Vekotren bestimmen Pfeilklassen

Question

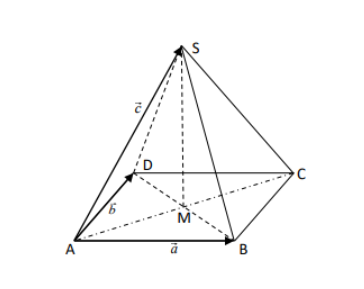
Aufgabe:

 \( 1) \) Drücke die gesuchten Vektoren als Summe (Differenz) der gegebenen Vektoren \( \vec{a}, \vec{b} \) und \( \vec{c} \) aus.
(Achtung: \( \vec{c} \) beschreibt nur eine der vier Seitenkanten, also z.B. \( \overrightarrow{C S} \neq \vec{c} \) ).

\( \overrightarrow{B S} ; \overrightarrow{C S} ; \overrightarrow{S D} ; \overrightarrow{S B} ; \overrightarrow{C M} ; \overrightarrow{S M} \)

Notiere die Lösungen auf dem Lösungsblattl

Answer 1

Nur Lösungsvorschläge zum Vergleichen.

Beim Vektor BS musst du dir gedanken machen wie du vom Punkt B zum Punkt s kommst idem du nur die Grundvektoren a, b und c benutzen darfst. Man könnte also zunächst a in umgekehrter Richtung gehen und dann c in korrekter Richtung. Der Term ist dann -a + c oder auch c - a.

BS = c - a
CS = c - a - b
SD = b - c
SB = a - c
CM = -1/2·(a + b)
SM = 1/2·(a + b) - c

Answer 2

Zum Beispiel \( \vec{BS} \) ist der Weg von B nach S entlang bekannter Vektoren, also \( \vec{a} \) in Gegenrichtung+\( \vec{c} \) = - \( \vec{a} \) +\( \vec{c} \).

So geht es auch in den anderen Fällen, wobei parallele, gleichlange, gleichgerichtete  Vektoren gleich sind.