hi
wir bestimmen die polarform der menge M = {w ∈ ℂ| |w| < 1, w = z-3i, z ∈ ℂ}.
z = x + yi
z-3i = x + yi - 3i = x + i(y-3)
|z-3i| = √(x² + (y-3)²)
|z-3i| < 1
√(x² + (y-3)²) < 1
x² + (y-3)² < 1² =
(x-0)² + (y-3)² < 1²
das ähnelt stark einer kreisgleichung vom typ (x-xm)² + (y-ym)² = r² mit dem mittelpunkt (0|3).
weil es aber eine ungleichung ist, können wir x und y innerhalb der intervalle
-1 < x < 1
und
2 < y < 4
variieren, solange die ungleichung erfüllt bleibt.
das ergibt eine menge von kreisen, die die ungleichung (x-0)² + (y-3)² < 1 erfüllen und zur menge M gehören, und
das ist wiederum eine kreisfläche, eine offene menge, die vom kreis x² + (y-3)² = 1
begrenzt wird und der nicht zu der gegebenen menge M gehört.
einen kreis mit dem radius r kann man in der komplexen ebene in polarform als re^{iφ} schreiben, mit 0 ≤ φ < 2π.
dieser kreis hat den mittelpunkt (0|0).
unser spezieller kreis, der die menge M umgibt/beschränkt hat den radius r = 1 und den mittelpunkt(0|3i).
jeder punkt des kreises re^{iφ} ist um 3i verschoben: re^{iφ} + 3i.
3i ist in polarform 3e^{i π/2}. die polarform des kreises, der die menge M beschränkt ist daher
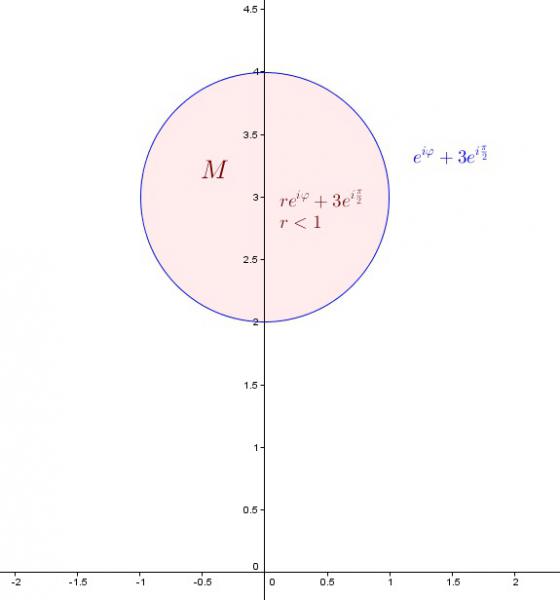
re^{iφ} + 3e^{i π/2} mit r = 1 und 0 ≤ φ < 2π.
damit haben wir die polarform der menge M mit M = {re^{iφ} ∈ ℂ| 0 <= r < 1, 0 ≤ φ < 2π} bestimmt.
weniger anschaulich kann man die intervalle formal berechnen:
x² + y² - 6y + 9 < 1
y² - 6y + x² + 8 < 0
y = 3 ± √(9-x²-8)
y = 3 ± √(1-x²)
1 - x² ≥ 0
x² ≤ 1
x1,2 ≤ ±1
wegen |z-3i| < 1
x1,2 < ±1
-1 < x < 1
y = 3 ± √(1-x²)
y1,2 = 3 ± 1
3 - √(1-x²) < y < 3 + √(1-x²)
und daraus die polarform bestimmen.
gruß
gorgar