Hallo fawick,
Die Gradienten hast Du ja schon bestimmt $$\begin{aligned}\nabla f(x,y) &= \begin{pmatrix} \frac{3x}{\sqrt{33+3x^2+4y^2}} \\ \frac{4y}{\sqrt{33+3x^2+4y^2}}{ } \end{pmatrix} \\ \nabla f(-2,1) &= \frac 17 \begin{pmatrix} -6\\ 4 \end{pmatrix} \\ \nabla g(x,y,z) &= \begin{pmatrix} 2xy - 3y^3 - 2z^3\\x^2 - 9xy^2 \\ 6z^2x \end{pmatrix} \\ \nabla g(2,1,-2) &= \begin{pmatrix} 17\\ -14\\ 48 \end{pmatrix}\end{aligned}$$Die Gleichung der Tangente \(t\) an die Fläche \(f\) resultiert aus dem Punkt und seinem Funktionswert und einem Richtunsvektor, der aus dem Gradienten und seiner Quadratesumme berechnet wird. $$\begin{aligned} t: \vec x &= \begin{pmatrix} x\\ y \\ f(x,y) \end{pmatrix} + r \begin{pmatrix} \nabla f \\ (\nabla f)^2\end{pmatrix} \\&= \begin{pmatrix} -2\\ 1\\ 7 \end{pmatrix} + r \begin{pmatrix} -6/7\\ 4/7\\ 52/49\end{pmatrix} \end{aligned}$$Zur Veranschaulichung habe ich Dir dazu eine Szene im Geoknecht3D erstellt
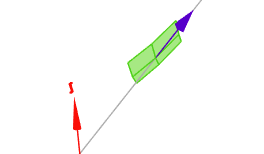
(klick auf das Bild, dann öffnet sich die Szene im Geoknecht3D)
Die kleine grüne Fläche - bestehend aus vier Vierecken - ist ein Ausschnitt aus \(f(x,y)\) in der Umgebung von \((-2;1;7)\). Der blaue Pfeil ist der Richtungsvektor aus der Geradengleichung. Der Richtungsvektor gibt die Richtung der größten Steigung der Tangentialebene an \(f\) in diesem Punkt an. Er wird über das Kreuzprodukt der beiden Steigungsvektoren aus dem Gradienten berechnet. Melde Dich bitte, wenn Du dazu Fragen hast.
Bei der Gleichung der Tangentialebene für eine Funktion \(g(x,y,z)\) mit drei Parametern bin ich mir unsicher. Ich vermute aber, dass sich die gesuchte Tangentialebene lediglich aus dem Gradienten als Normalenvektor und dem Parametervektor \(\vec p = (2;1;-2)\) als Aufpunkt ableitet. Das sähe dann so aus: $$\begin{aligned} E: \space \nabla g(x,y,z) \cdot \vec x &= \nabla g(x,y,z) \cdot \vec p \\ \begin{pmatrix} 17\\ -14\\ 48 \end{pmatrix} \cdot \vec x &= \begin{pmatrix} 17\\ -14\\ 48 \end{pmatrix} \cdot \begin{pmatrix} 2\\ 1\\ -2 \end{pmatrix} = -76 \end{aligned}$$
Für die Gleichung der Tangentialebene an die Fläche \(\sqrt z = f(x,y)\) hatte MathePeter ja bereits einen Vorschlag gemacht. Ich verfolge einen etwas anderen Ansatz - gehe natürlich davon aus, dass das Ergebnis das gleiche ist. Mit \(\sqrt z = f\) ist$$\begin{aligned} z &= 33+3x^2 + 4y^2, \quad z(-2,-1) = 49 \\ \nabla z &= \begin{pmatrix} 6x \\ 8 y\end{pmatrix} \\ \nabla z(-2,-1) &= \begin{pmatrix} -12\\ -8 \end{pmatrix} \end{aligned}$$Die beiden Steigungsvektoren der Funktion \(z(x,y)\) sind demnach$$u_x = \begin{pmatrix} 1\\ 0\\ -12 \end{pmatrix}, \quad u_y = \begin{pmatrix} 0\\ 1\\ -8 \end{pmatrix}$$ diese beiden Vektoren ziehen die Tangentialfläche auf. Für die Normalform der Ebene benötigt man dann das Kreuzprodukt und den Aufpunkt \((-2; -1; z(-2;-1))\):$$ u_x \times u_y = \begin{pmatrix} 1\\ 0\\ -12 \end{pmatrix} \times \begin{pmatrix} 0\\ 1\\ -8 \end{pmatrix} = \begin{pmatrix} 12\\ 8\\ 1\end{pmatrix}\\ E: \space\begin{pmatrix} 12\\ 8\\ 1\end{pmatrix} \cdot \vec x = \begin{pmatrix} 12\\ 8\\ 1\end{pmatrix}\cdot \begin{pmatrix} -2\\ -1\\ 49\end{pmatrix} = 19$$Da habe ich auch eine Szene zu erstellt, damit man sehen kann, dass die Ergebnisse sinnvoll sind ;-)
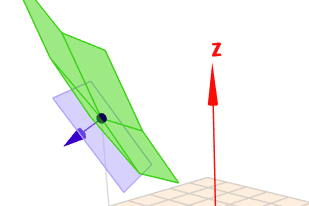
das ganze ist in Z um den Faktor 10 geschrumpft, damit es noch auf das Bild passt. Und der Normalenvektor ist negativ und auf 1 normiert. Die grünen Vierecke sind wieder ein Aussschnitt aus \(z(x,y)\) und die blaue Ebene ist die berechnete Tangentialebene.