Materialverbrauch nur mit Volumen rausfinden

Question

Eine Dose soll eine Flüssigkeitsmenge von 330ℓ beinhalten. Wer findet diejenige Höhe h und den Durchmesser d, bei dem der Materialverbrauch (sprich: die Oberfläche) möglichst gering wird?! Löse durch Probieren! 
Hinweis: 1ℓ = 1³

Gerne kann mir jemand dazu ein Verfahren dazu erklären.

Liebe Grüße

Berris

Answer 1

Ein Zylinder mit gegebenem Volumen soll eine minimale Oberfläche haben.

Nebenbedingung

V = pi·r^2·h
h = V/(pi·r^2)

Hauptbedingung

O = 2·pi·r·h + 2·pi·r^2
O = 2·pi·r·(V/(pi·r^2)) + 2·pi·r^2
O = 2·pi·r^2 + 2·V/r

Extremstellen O' = 0

O' = 4·pi·r - 2·V/r^2 = 0 → r = (V/(2·pi))^(1/3)

h = V/(pi·r^2) = V/(pi·((V/(2·pi))^(1/3))^2) = (4·V/pi)^(1/3) = 2·r

O = 2·pi·((V/(2·pi))^(1/3))^2 + 2·V/((V/(2·pi))^(1/3)) = (54·pi·v^2)^(1/3)

Comments

Danke für die schnelle Antwort ich hab ein änderes Ergebnis durch probieren raus und kann es mir nicht ganz erklären.Vlt könnten sie es sich anschauen

Liebe Grüße

O= 2*(5,5)^2 +2*∏*(5,5)*330/∏*(5,5)^2=180,5 cm^2

Lieben Dank

---

O= 2*(5,5)2 +2*∏*(5,5)*330/∏*(5,5)2=180,5 cm2

Was soll ich dazu sagen. Bei so einer Geringen Oberfläche haben da niemals 330 Liter Platz.

Bei einer Lösung über Probieren Erwarte ich eigentlich eine Wertetabelle für verschiedene Radien.

Rechne mal zu jeder Aufgeführten Dose das Volumen und die Oberfläche nach.

Answer 2

$$ V=\pi r^2 h ~~;~~ \mathcal O=2\pi r ( r + h)$$

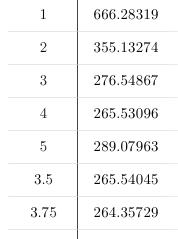
$$330\,\ell = \pi r^2 h \Rightarrow h=\frac{330\,\ell}{\pi r^2}\\ \Rightarrow \mathcal O=2\pi r^2 + 2\pi r\cdot\frac{330\,\ell}{\pi r^2} \Rightarrow \mathcal O=2\pi r^2 + \frac{660\,\ell}{ r} $$

Für verschiedene Radien in dm erhält man die Oberflächen in dm^2: