Aufgabe:
Ein Verbindungsstück für 2 Rohre soll untersucht werden.
Das Verbindungsstück ist rotationssymmetrisch bezüglich der \( x \) -Achse. Die obere Begrenzungskurve der Schnittfläche, die in der nachstehenden Grafik schraffiert dargestellt ist, wird durch die Funktionsgleichung \( y=2+\frac{x^{2}}{2}-\frac{x^{4}}{4} \) beschrieben, wobei \( x \) und \( y \) Längen in Dezimetern beschreiben. Der innere Durchmesser des Verbindungsstückes ist \( d=2 \mathrm{dm} \)
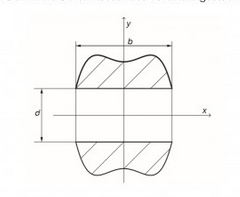
- Berechnen Sie die Breite \( b \) des Verbindungsstückes.
- Erstellen Sie eine Formel zur Berechnung des Volumens des Verbindungsstúckes mithilfe der Integralrechnung.
Ich verstehe nicht, wieso in der Lösung zu Punkt 2 das steht:
Formel zur Berechnung des Volumens:
\( V=\pi \cdot \int \limits_{-1.8}^{1,8} y^{2} d x-1^{2} \cdot \pi \cdot 2 \cdot 1,8 \)
Der erste Teil berechnet ja das Volumen von dem gewölbten Stück da oben, ist mir klar
aber wie kommt man auf -1^2*pi*2*1.8 ?