Welcher der folgenden Ansätze ist der richtige, um das Volumen einer Vase zu errechnen, welche aus dem Zwischenraum zweier Funktionen besteht (s. Bild)? Was errechnet man mit dem falschen Ansatz?
Ansatz 1:
$$π*\int_{0}^{4}(f(x))^2dx-π*\int_{0}^{4}(g(x))^2dx$$
Ansatz 2:
$$π*\int_{0}^{4}(f(x)-g(x))^2dx$$
Bild:
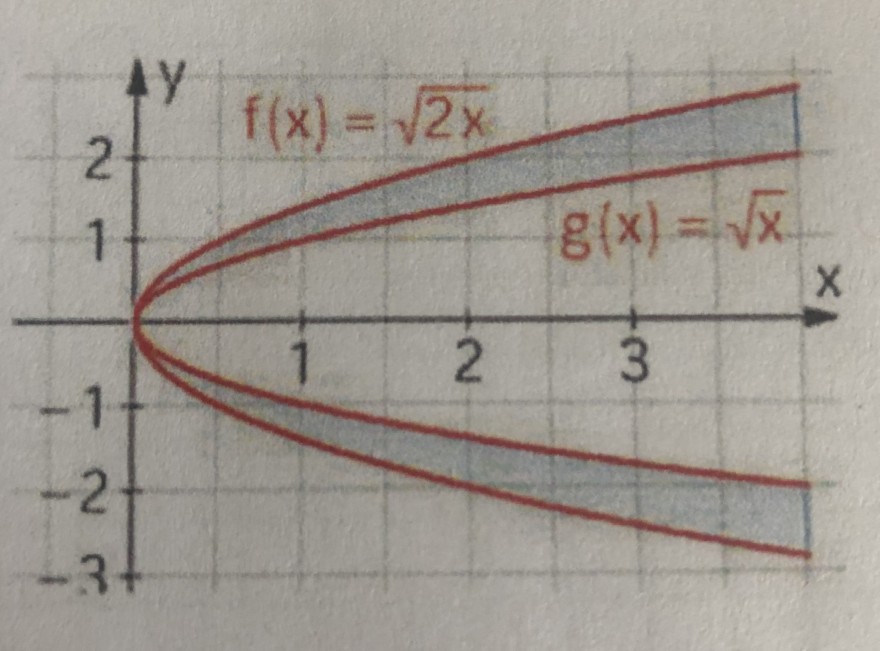
Text erkannt:
\( \frac{2}{1} \frac{f^{y} f(x)=\sqrt{2 x}}{\frac{-1}{-2}} \frac{8(x)=\sqrt{x}}{-3} \)