Additionstheoreme Beweisen für Alpha,Beta (0, Pi/2), aber alpha + beta > pi/2

Question

Aufgabe:

Beweisen Sie die Additionstheoreme für den Fall $\alpha, \beta \in\left(0, \frac{\pi}{2}\right),$ aber $\alpha+\beta>\frac{\pi}{2}$

$$\begin{array}{l} \sin (\alpha+\beta)=\sin (\alpha) \cos (\beta)+\cos (\alpha) \sin (\beta) \\ \cos (\alpha+\beta)=\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta) \end{array}$$

Ich finde nur Beweise mit komplexen Zahlen oder über die Eulersche Funktion. Beides wurde jedoch in der Vorlesung nicht behandelt, daher bin ich komplett planlos. Beweis der Additionstheoreme in der Vorlesung ging über rechtwinklige Dreiecke im Einheitskreis.

Comments

Vom Duplikat:

Titel: Beweisen Sie die Additionstheoreme für den Fall α,β∈(0,π2), aber α+β>π2

Stichworte: beweise

Beweisen Sie die Additionstheoreme für den Fall $\alpha, \beta \in\left(0, \frac{\pi}{2}\right),$ aber $\alpha+\beta>\frac{\pi}{2}$
$$\begin{array}{l} \sin (\alpha+\beta)=\sin (\alpha) \cos (\beta)+\cos (\alpha) \sin (\beta) \\ \cos (\alpha+\beta)=\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta) \end{array}$$

---

" aber α+β>π2 "

Was meinst du denn damit genau? Soll etwas hochgestellt sein? Oder echtes Duplikat und richtig zusammengefügt?

Answer 1

Aloha :)

Eine Drehung in der xy-Ebene um den Winkel $\alpha$ wird durch eine Drehmatrix realisiert:$$D_\alpha=\begin{pmatrix}\cos\alpha & -\sin\alpha\\\sin\alpha & \cos\alpha\end{pmatrix}$$Das wird aus dem Transformationsverhalten der Basisvektoren klar:$$\binom{1}{0}\to\binom{\cos\alpha}{\sin\alpha}\quad;\quad\binom{0}{1}\to\binom{-\sin\alpha}{\cos\alpha}$$Es handelt sich also um eine Drehung um den Winkel $\alpha$ entgegen dem Uhrzeigersinn um den Koordinatenursprung.

Die Hintereinanderausführung von 2 Drehungen, zuerst um den Winkel $\alpha$ und danach um den Winkel $\beta$ wird durch eine Matrix-Multiplikation realisert $D_{\alpha+\beta}=D_\beta\cdot D_\alpha$:$$\begin{pmatrix}\cos(\alpha+\beta) & -\sin(\alpha+\beta)\\\sin(\alpha+\beta) & \cos(\alpha+\beta)\end{pmatrix}$$$$\quad=\begin{pmatrix}\cos\beta & -\sin\beta\\\sin\beta & \cos\beta\end{pmatrix}\begin{pmatrix}\cos\alpha & -\sin\alpha\\\sin\alpha & \cos\alpha\end{pmatrix}$$$$\quad=\begin{pmatrix}\cos\alpha\cos\beta-\sin\alpha\sin\beta & -\sin\alpha\cos\beta-\cos\alpha\sin\beta\\\sin\alpha\cos\beta+\cos\alpha\sin\beta & \cos\alpha\cos\beta-\sin\alpha\sin\beta\end{pmatrix}$$Vergleich der Matrix-Elemente liefert die Behauptungen.

Comments

Super, dankeschön. Jetzt habe ich es verstanden

Answer 2

Beweis eines Additionstheorems
Zu zwei vorgegebenen Winkeln α und β mit (α+β)< 180° sei ein Parallelogramm ABDC so gewählt, dass eine Diagonale AC des Parallelogramms ABCD mit den Seitenlängen a und b einen Innenwinkel in α und β teilt. Außerdem sei die Längeneinheit so gewählt, dass b=1. Nach der Definition von sin und cos gelten dann die folgenden Bezeichnungen:

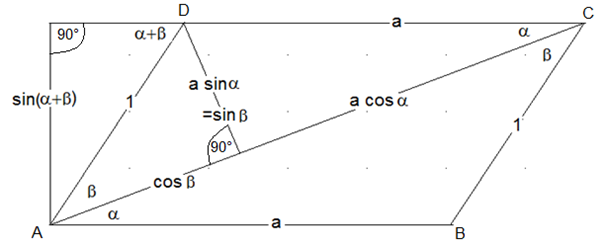
Der Flächeninhalt des Parallelogramms ist dann einerseits a·sin(α+β), andererseits zerlegt die Diagonale AC das Parallelogramm in zwei kongruente Dreiecke, die zusammen den Flächeninhalt (cosβ+acosα)·a·sinα haben. Also gilt:

a·sin(α+β) = (cosβ+a·cosα)·a·sinα und nach Division durch a
sin(α+β) = (cosβ+a·cosα)·sinα=sinα·cosβ+ sinα·a·cosα und wegen sinαa = sinβ gilt dann
sin(α+β) =sinα·cosβ+ sinβ·cosα.