Analysis, lösen von Gleichung mit a

Question

 Aufgabe: Wir haben eine ganzrationale Funktion g vierten Grades.

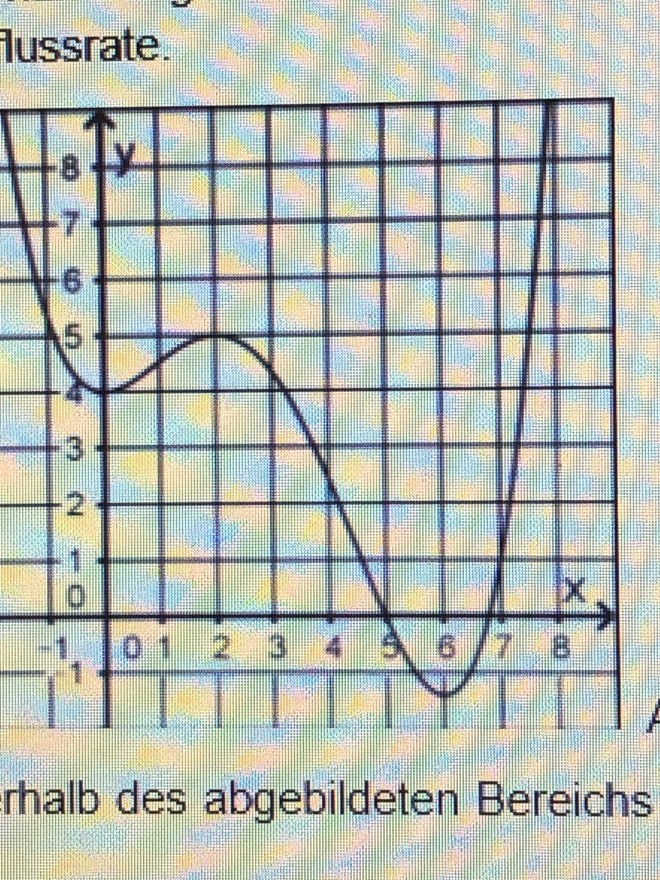
Betrachtet wird die Gleichung g(x)=a mit a ∈ℝ. Geben sie die Werte für a an, für die die gleichung genau drei lösungen hat.

Die Lösung wäre a= 4 und a=5. Wie kommt man auf das Ergebnis? wie muss ich die Aufgabe rechnen? Danke für eure Hilfe

Text erkannt:

\( \sqrt{ } \)

Answer 1

Die Lösung wäre a= 4 und a=5. Wie kommt man auf das Ergebnis? wie muss ich die Aufgabe rechnen?

Hier soll nichts gerechnet werden. Denke dir die konstante Funktion y=a für verschiedene a in die Zeichnung hinein. Die jeweilige Anzahl der Schnittstellen des Graphen von g mit der Geraden y=a sind genau die Lösungen der Gleichung g(x)=a. Für welche a gibt es genau drei Schnittstellen?

Answer 2

Drei Nullstellen gibt es, wenn der gegebene Graph um 4 Einheiten nach unten verschoben wird, sodass das linke Minimum auf der x-Achse liegt. Leider fehlt die Funktionsgleichung.

Comments

Ja , es wurde keine Funktionsgleichung angegeben.