Wie kann man diese Aufgabe beweisen?

Question

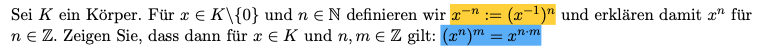
Text erkannt:

Sei \( K \) ein Körper. Für \( x \in K \backslash\{0\} \) und \( n \in \mathbb{N} \) definieren wir \( x^{-n}:=\left(x^{-1}\right)^{n} \) und erklären damit \( x^{n} \) für \( n \in \mathbb{Z} . \) Zeigen Sie, dass dann für \( x \in K \) und \( n, m \in \mathbb{Z} \) gilt: \( \left(x^{n}\right)^{m}=x^{n \cdot m} \)

Answer 1

Hallo

 für positive n,m stimmt die Regel nach definition der Potenzfunktion x^n als Abkürzung für das n fache Produkt von x.  dann für negative Zahlen wende es auf x^-1an

Gruß lul