Bestimmen Sie die (exakten) Winkel \beta, \gamma und \delta im Bogenmaß.

Question

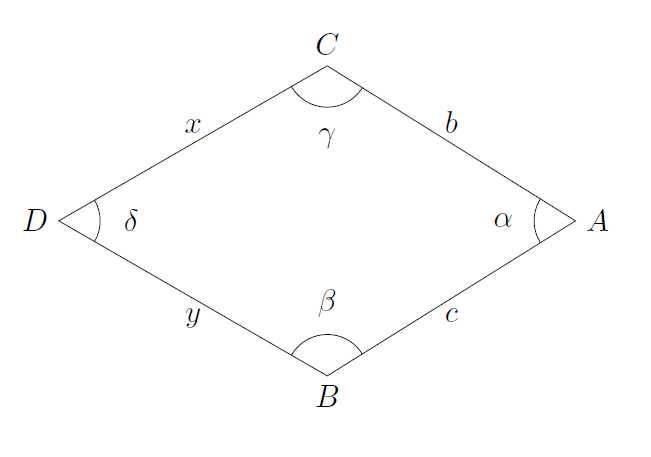
Das ist kein parallelogramm

Gegeben sei ein Viereck mit den gleichen Bezeichnungen in der Abbildung. Nun seien
$$ \alpha=\frac{\pi}{2}, \quad c=3, \quad b=\sqrt{27}, \quad x=\sqrt{108}, \quad y=12 $$

gegeben. Bestimmen Sie die (exakten) Winkel \( \beta, \gamma \) und \( \delta \) im Bogenmaß.

Answer 1

Das Dreieck ABC ist rechtwinklig mit rechtem Winkel bei A. Mit Pythagoras kann man daher die Länge von BC berechnen.

Anhand der Längen BC, x und y kann man mit Pythagoras feststellen, dass das Dreieck BCD auch rechtwinklig ist mit rechtem Winkel bei C.

Der Rest ist Trigonometrie.

Comments

Wie kann ich feststellen, dass das Dreieck BCD rechtwinkelig ist??

---

Dazu musst du natürlich vorher BC berechnet haben.

Der Satz des Pythagoras hat zwei Richtungen:

1. Wenn das Dreieck mit den Seiten a, b, c rechtwinklig ist und c die Hypotenuse ist, dann ist a² + b² = c².
   
2. Wenn in einem Dreieck mit kurzen Seiten a, b und längster Seite c die Beziehung a² + b² = c² gilt, dann ist das Dreieck rechtwinklig und c ist die Hypotenuse.

Diese zweite Richtung benötigst du dazu.

---

BC habe ich schon längst berechnet!!!! und für delta habe ich 30 grad raus! Ich weiß nicht ob es richtig ist und für bc habe ich 6 raus

---

und für delta habe ich 30 grad raus!

Das ist richtig, muss natürlich noch in Bogenmaß umgerechnet werden.

und für bc habe ich 6 raus

Und es ist 12² = 6² + (√108)².

---

WIE BEKOMME ICH BETTA UND GAMMA RAUS???

---

γ = γ₁ + γ₂ wobei γ₁ der Winkel bei C im Dreieck ABC ist und γ₂ der Winkel bei C im Dreieck BCD.

β kannst du dann über die Winkelsumme im Viereck berechnen.

---

wie bekomme ich y2 raus???

---

Ich erinnere mal an meine Antwort: "dass das Dreieck BCD auch rechtwinklig ist mit rechtem Winkel bei C."

---

woher weiß ich dass, das dreieck an der stelle c rechtwinkling ist????????

---

Wir drehen uns hier ein wenig im Kreis. Das ist genau die gleiche Frage wie die im ersten Kommentar.

---

ja genau, weil ich es immer noch nicht verstanden habe..

---

Die zweite Richtung vom Satz des Pythagoras in Verbindung mit

        12² = 6² + (√108)².