Wie groß sind die Winkel \beta, \gamma und \delta?

Question

Aufgabe:

Text erkannt:

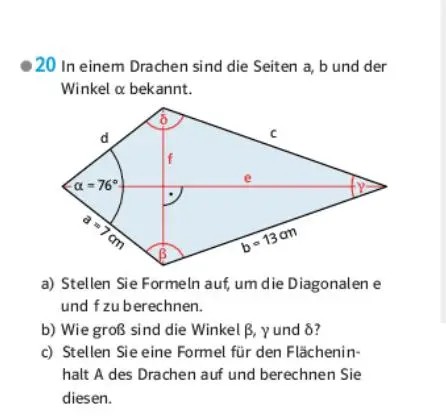
20 In einem Drachen sind die Seiten a, b und der Winkel \( \alpha \) bekannt.
a) Stellen Sie Formeln auf, um die Diagonalen e und \( f \) zu berechnen.
b) Wie groß sind die Winkel \( \beta, \gamma \) und \( \delta \) ?
c) Stellen Sie eine Formel für den Flächeninhalt A des Drachen auf und berechnen Sie diesen.

Problem/Ansatz:

Ich verstehe nicht so ganz, wie man die Diagonale e und f berechnen soll?

Answer 1

f = 2·7·SIN(76°/2) = 8.619260654

e = √(7^2 - (8.619260654/2)^2) + √(13^2 - (8.619260654/2)^2) = 17.78094732

Comments

Beschäftige dich auch bitte mit der sehr guten Antwort von oswald, die dich auch zur Lösung bringt. Verwende mein Lösungsvorschlag dann nur zur Kontrolle.

---

f = 2·7·SIN(76°/2) = 8.619260654
e = √(72 - (8.619260654/2)2) + √(132 - (8.619260654/2)2) = 17.78094732

ich finde es immer wieder überraschend, dass sich Fragesteller mit Antworten dieser Art anscheinend zufrieden stellen lassen.

@ BeitlerE: was steht denn in dieser Antwort, was Du vorher nicht gewußt hast?

---

ich habe es mir schwieriger vorgestellt gehabt.

---

ich habe es mir schwieriger vorgestellt gehabt.

es beantwortet zwar nicht meine Frage - aber ok!

Answer 2

Löse das Gleichungssystem

        \(\begin{aligned}\frac{f/2}{a}&=\sin\frac{\alpha}{2}\\e_1^2 + \left(\frac{f}{2}\right)^2&=a^2\\e_2^2 + \left(\frac{f}{2}\right)^2&=b^2\\e_1+e_2&=e\end{aligned}\).

Comments

vielen dank oswald für dein Gleichungssystem. So könnte ich nächstes Mal auch anfangen. :) Liebe Grüße.