Aufgabe: Wie kann ich g machen. f(x)=f(x):=1/1280x^4-1/10x^2+16/5
Beim Ausbau des Dachgeschosses wird zunächst eine Wärmedämmung auf den Boden des Dachgeschosses aufgebracht (schwarz gezeichnete Fläche in Abbildung 3). Diese Wärmedämmung hat eine Dicke von 20 cm.
In den verbleibenden Raum zwischen der oberkante der Wärmedämmung und der Giebellinie soll ein Wohnraum eingebaut werden, dessen rechteckige Stirnseite (schraff. Fläche in Abbildung 3) möglichst groß sein soll. Dafür müssen die Koordinaten des Punktes P (x|f(x)) auf dem Graphen f bestimmt werden, für den der Flächeninhalt des achsenparallelen Rechtecks mit dem Eckpunkt P (schraffierte Fläche in Abbdildung 3) maximal wird.
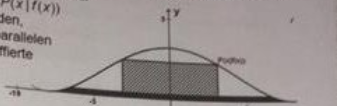
g) Das Planungsbüro, das die Baumaßnahmen in dem Dachgeschoss vorbereitet, schlägt vor, den Wohnraum mit einer geneigten Decke zu bauen.
Die Lage der Decke wird auf der rechten Seite durch die Geraden zwischen den Punkten Q (0 | 3) und R (5 | 1) festgelegt.
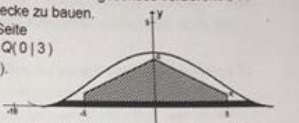
Ermitteln Sie den maximalen vertikalen Abstand zwischen dieser Geraden und der Giebellinie im Bereich \( [0 ; 5] \)
Hinweis: Es genügt die Verwendung der notwendigen Bedingung