Also ja!
Text erkannt:
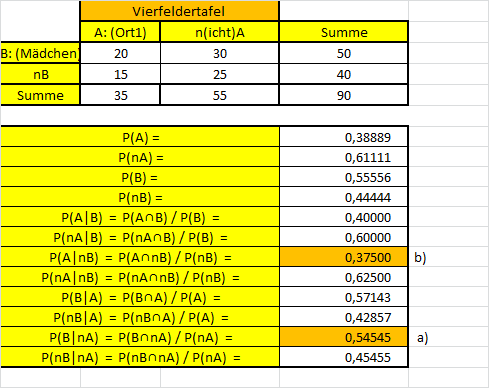
\begin{tabular}{c|c|c|c|}
\multirow{2}{*} {} & \multicolumn{2}{|c|} { Vierfeldertafel } & \\
\cline { 2 - 3 } & A: (Ort1) & n(icht)A & Summe \\
\hline B: (Mädchen & 20 & 30 & 50 \\
\hline nB & 15 & 25 & 40 \\
\hline Summe & 35 & 55 & 90 \\
\hline
\end{tabular}
\begin{tabular}{c|c|}
\hline\( P(A)= \) & 0,38889 \\
\hline\( P(n A)= \) & 0,61111 \\
\hline\( P(B)= \) & 0,55556 \\
\hline\( P(n B)= \) & 0,44444 \\
\hline\( P(A | B)=P(A \cap B) / P(B)= \) & 0,40000 \\
\hline\( P(n A | B)=P(n A \cap B) / P(B)= \) & 0,60000 \\
\hline\( P(A | n B)=P(A \cap n B) / P(n B)= \) & 0,37500 \\
\hline\( P(n A | n B)=P(n A \cap n B) / P(n B)= \) & 0,62500 \\
\hline\( P(B | A)=P(B \cap A) / P(A)= \) & 0,57143 \\
\hline\( P(n B | A)=P(n B \cap A) / P(A)= \) & 0,42857 \\
\hline\( P(B | n A)=P(B \cap n A) / P(n A)= \) & 0,54545 \\
\hline\( P(n B | n A)=P(n B \cap n A) / P(n A)= \) & 0,45455 \\
\hline
\end{tabular}