Hallo,
in dem 'Durchstoßpunkt' bzw. im Schnittpunkt von Gerade \(g\) und Ebene \(E\) müssen die Koordinaten des Punktes sowohl die Ebenengleichung als auch die Geradengleichung erfüllen. Um diesen Punkt zu finden, setzt man daher die Geradengleichung $$g: \space \vec x = \begin{pmatrix}-1\\ -7\\ -2\end{pmatrix} + r \begin{pmatrix}1\\ 3\\ 2\end{pmatrix}$$ in die Ebenengleichung $$E: \space x-5y-4z=-2 \quad \Leftrightarrow \quad \begin{pmatrix}1\\ -5\\ -4\end{pmatrix} \vec x = -2$$ ein. Dann erhält man$$\begin{aligned} \begin{pmatrix}1\\ -5\\ -4\end{pmatrix} \left( \begin{pmatrix}-1\\ -7\\ -2\end{pmatrix} + r \begin{pmatrix}1\\ 3\\ 2\end{pmatrix}\right) &= -2 \\ 1 \cdot (-1) + (-5)\cdot (-7) + (-4) \cdot (-2) \\ + r (1 \cdot 1 + (-5) \cdot 3 + (-4) \cdot 2) & = -2 \\ 42 - 22r &= -2 \\ 22r &= 44 \\ r& = 2\end{aligned} $$D.h. für \(r=2\) erfüllen die drei Koordinaten \(x\), \(y\) und \(z\) beide Gleichungen und daher ist der Schnittpunkt \(S\) $$\begin{aligned} S = \vec x(r=2) &= \begin{pmatrix}-1\\ -7\\ -2\end{pmatrix} + 2 \begin{pmatrix}1\\ 3\\ 2\end{pmatrix} \\ &= \begin{pmatrix}-1\\ -7\\ -2\end{pmatrix} + \begin{pmatrix}2\\ 6\\ 4\end{pmatrix} \\&= \begin{pmatrix}1\\ -1\\ 2\end{pmatrix} \end{aligned}$$Graphisch sieht das ganze wie folgt aus:
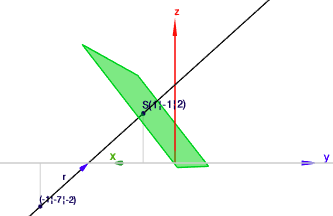
klick auf das Bild, dann öffnet sich die Szene im Geoknecht3D und Du bekommst einen besseren räumlichen Eindruck.
Gruß Werner