Aufgabe:
Aufgabe:
Aufgrund ergiebiger Regenfälle wurde in der zweiten Oktoberhälfte 2016 am Rhein ein Ansteigen des Wassers beobachtet.
Am 20.10.2016 um 0:00 Uhr wurde an der Messstelle in Bonn ein Wasserstand \( ^{1} \) von \( 130 \mathrm{cm} \) gemessen. Das Wasser begann dann zu steigen und nach einiger Zeit zunächst wieder zu sinken.
Eine Schülerin verwendet die auf \( \mathbb{R} \) definierte Funktion \( h \) mit der Funktionsgleichung
\( h(t)=-\frac{80}{27} \cdot t^{3}+\frac{40}{3} \cdot t^{2}+130 \)
für \( 0 \leq t \leq 3,5, \) um den Wasserstand des Rheins an der Messstelle in Bonn im Zeitraum vom 20.10.2016, 0:00 Uhr, bis zum 23.10.2016, 12:00 zu modellieren.
Dabei entspricht z. B. \( t=0 \) der Zeit 0: 00 Uhr am \( 20.10 .2016, t=1 \) der Zeit 0: 00 Uhr am 21.10 .2016 und \( t=3,5 \) der Zeit 12: 00 Uhr am \( 23.10 .2016 . h(t) \) ist der Wasserstand des Rheins an der Messstelle in Bonn in cm.
Der Graph von \( h \) ist in der Abbildung 2 dargestellt.
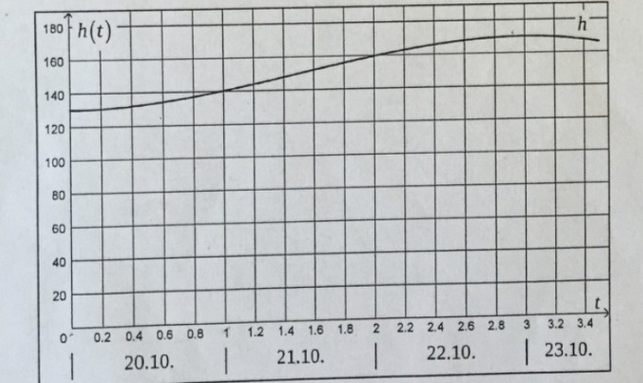
Mit der Funktion h ist es möglich, die Aufgaben a) bis d) zu bearbeiten.
a) Berechnen Sie den Wasserstand des Rheins an der Messstelle in Bonn am 21.10.2016 um 12:00 Uhr.
b) Berechnen Sie \( \frac{h(3)-h(1)}{2} \) und interpretieren Sie den berechneten Wert im Sachzusammenhang.
c) Ermitteln Sie rechnerisch den niedrigsten und höchsten Wasserstand im betrachteten Zeitraum.
d) Bestimmen Sie rechnerisch, wie lange der Wasserstand im betrachteten Zeitraum zwischen \( 140 \mathrm{cm} \) und \( 150 \mathrm{cm} \) lag.