Seien g,h zwei Geraden auf der Einheitssphäre, die sich im Punkt P schneiden

Question

Aufgabe:

Seien \( g, h \) zwei Geraden auf der Einheitssphäre, die sich im Punkt \( P \) schneiden. Seien weiter\( \operatorname{hin} E_{g} \) und \( E_{h} \) die zugehörigen Ebenen und \( \mathfrak{g} p, \mathfrak{h}_{P} \) die Tangenten an \( g \) bzw. \( h \) im Punkt \( P \).
Zeigen Sie, dass der Winkel zwischen \( \mathfrak{g}_{P} \) und \( \mathfrak{h}_{P} \) gleich dem Winkel zwischen \( E_{g} \) und \( E_{h} \) ist.

Problem/Ansatz:

Ich bin bei dieser Aufgabe komplett Planlos und habe keine Idee wie ich da ran gehen soll.

Comments

Vom Duplikat:

Titel: Zeigen Sie, dass der Winkel zwischen gP und hP gleich dem Winkel zwischen Eg und Eh ist.

Stichworte: geometrie

Seien \( g, h \) zwei Geraden auf der Einheitssphäre, die sich im Punkt \( P \) schneiden. Seien weiter\( \operatorname{hin} E_{g} \) und \( E_{h} \) die zugehörigen Ebenen und \( \mathfrak{g}_{P}, \mathfrak{h}_{P} \) die Tangenten an \( g \) bzw. \( h \) im Punkt \( P \)
Zeigen Sie, dass der Winkel zwischen \( \mathfrak{g}_{P} \) und \( \mathfrak{h}_{P} \) gleich dem Winkel zwischen \( E_{g} \) und \( E_{h} \) ist.

---

Bitte Fragen nur einmal absenden?

Welche Version ist die Definitive?

---

Geraden auf der Einheitssphäre werden in der Regel als Grosskreise definiert. Bei euch auch?

Answer 1

Hallo,

bin bei dieser Aufgabe komplett Planlos

Hilft folgendes Bild ?:

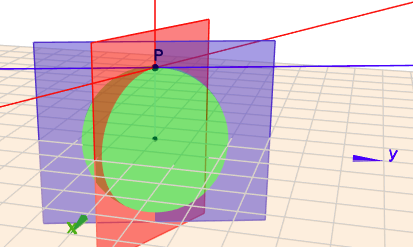
(klick drauf, dann kanst Du die Szene mit der Maus drehen)

Ein Versuch:

\(p\) sei der Vektor vom Mittelpunkt zum Punkt \(P\). \(n_1\) und \(n_2\) sind die Normalenvektoren der Ebenen - und seien jeweils Einheitsvektoren. Der Winkel \(\alpha\) zwischen den Ebenen folgt somit aus dem Skalarprodukt$$\cos \alpha = \left< n_1, n_2\right>, \quad |n_1| = |n_2| = 1$$Die Richtungsvektoren \(t_i\) der Tangenten in \(P\) lassen sich berechnen aus$$t_i = p \times n_i, \quad i \in \{1,\,2\}$$Da \(n_i \perp p\) und \(|p|=1\) ist \(|t_i| = 1\). Der Winkel \(\beta\) zwischen den beiden Richtungsvektoren (und damit zwischen den Tangenten) folgt also auch aus $$\begin{aligned}\cos \beta &= \left< t_1, t_2\right> \\  &= \left< p \times n_1 ,\, p \times n_2\right> \\ &= \underbrace{\left< p, p\right>}_{=1} \cdot \left< n_1, n_2\right> - \underbrace{\left< n_1, p \right> }_{=0} \cdot \underbrace{\left< p, n_2\right> }_{=0} &&\left| \,\text{*)}\right. \\ &= \left< n_1, n_2\right> \\&= \cos \alpha\end{aligned}$$ zu *) siehe Lagrange Identität.

Comments

Ja, so hab ich mir das auch vorgestellt.

Kann aber damit auch nichts weiter anfangen.

Mit Ebenen haben wir bisher nicht gearbeitet. Das ganze kommt gerade irgendwie aus dem nichts

---

Hallo,

wenn man sich das Bild oben anschaut, so ist doch offensichtlich, dass die beiden Tangenten im gleichen Winkel zu einander stehen wie die beiden Ebenen.

Mit Ebenen haben wir bisher nicht gearbeitet.

.. mit was habt Ihr denn bisher gearbeitet. Auf was kann man aufsetzen? Welche Definitionen oder Sätze im Kontext der Einheitssphäre habt Ihr bisher gehabt.

Was ist "Gerade auf der Einheitssphäre" und "zugehörige Ebene" ?

---

.. Antwort dahin gehend erweitert.

---

Was ist "Gerade auf der Einheitssphäre" und "zugehörige Ebene" ?

Vermutlich ein Großkreis und seine Trägerebene.

Ach - steht ja schon oben.