Ich greife nochmal Rolands Lösung auf:
Der rechte Winkel wird im Punkt C gewählt. Also gilt für den Flächeninhalt des Dreiecks
$$\frac{a\cdot b}{2}=336\quad |\cdot 2\\a\cdot b=672$$ $$tan(\beta)=\frac{\text{Gegenkathete}}{\text{Ankathete}}\\tan(73,74)=\frac{b}{a}\\3,43=\frac{b}{a}\quad |\cdot a\\ 3,43a=b$$
Das setzt du für b in die 1. Gleichung ein:
$$a\cdot 3,43a=672\\ 3,43a^2=672\quad |:3,43\\ a^2=195,92\quad |\sqrt{}\\ a\approx14$$ $$b=3,43\cdot a=3,43\cdot 14\approx 48$$ $$sin(\beta)=\frac{b}{c}\\sin(73,74)=\frac{48}{c}\\ 0,96=\frac{48}{c}\\0,96c=48\\c=50$$
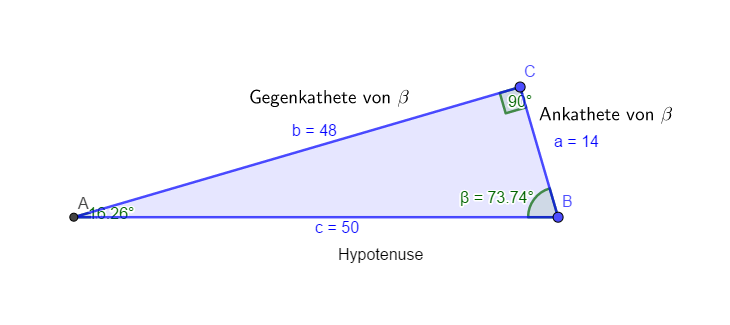 Kannst du das nachvollziehen?
Kannst du das nachvollziehen?