Allgemeines und gleichschenkliges Dreieck. Welche Behauptung sollte bewiesen werden? Wo liegt die Fehlerursache?
Nachfolgend finden Sie einen fehlerhaften Beweis abgedruckt. Welche Behauptung sollte bewiesen werden? Untersuchen Sie die einzelnen Beweisschritte: Begründen Sie, ob ein Beweisschritt richtig oder falsch ist. Wo liegt die Fehlerursache?
Hallo liebe Leute, der Beweis ist nur ein Besipiel, und den habe ich auch nicht gemacht. Wir sollen nur die Fehler im Beweis aufzählen.
EDIT: Originalfrage im Bild (im Kommentar) bitte nicht zerstören.
Aufgabe:
Wir betrachten ein allgemeines Dreieck ABC. Die Winkelhalbierende g des Winkels \( \prec \) BAC und die Mittelsenkrechte h der Strecke (BC) schneiden sich im Punkt P. Von P aus konstruieren wir die Senkrechten auf AB und \( A C ; \) die Lotfußpunkte sind \( D \) und \( E \) (siehe Skizze)
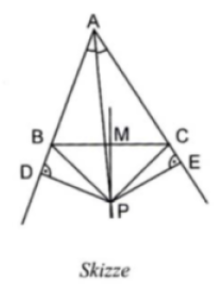
\( \overline{\mathrm{PD}}=\overline{\mathrm{PE}} \quad \) (Eigenschaft der Winkelhalbierenden)
\( \overline{\mathrm{PB}}=\overline{\mathrm{PC}} \quad \) (Eigenschaft der Mittelsenkrechten)
\( \prec \mathrm{PDB}=\prec \mathrm{CEP}\left(=90^{\circ}, \text { laut Konstruktion }\right) \)
\(\Downarrow\)
\( \Delta P D B \cong \Delta C E P \quad[\text { Ssw }] \)
\(\Downarrow\)
\( \overline{\mathrm{BD}}=\overline{\mathrm{CE}} \) (1)
\( \overline{\mathrm{AP}}=\overline{\mathrm{AP}} \quad(\text { gemeinsame Seite }) \)
\( \prec\mathrm{DAP}=\prec \mathrm{PAE} \) (Angabe)
\( \prec \mathrm{PDA}=\prec \mathrm{AEP}\left(=90^{\circ}, \text { laut Konstruktion }\right) \)
\(\Downarrow\)
\( \Delta P D A \cong \Delta P E A \quad [sww]\)
\(\Downarrow\)
\( \overline{A D}=\overline{A E} \) (2)
aus (1) und (2) folgt
\( \overline{\mathrm{AB}}=\overline{\mathrm{AC}} \)
Dies bedeutet: Das allgemeine Dreieck ist zwangsläufig gleichschenklig.
Widerspruch!