Aufgabe:
Eine Firma baut Sprungschanzen für BMX-Fahrer in verschiedenen Formen, deren seitliches Profil jeweils durch den Graphen einer Funktion \( f_{a} \) mit der Gleichung
$$ f_{a}(x)=-\frac{1}{4 \cdot a^{2}} x^{3}+\frac{3}{4} x, \quad-8 \leq x \leq 0,^{1} $$
beschrieben wird mit \( 3,2 \leq a \leq 4\left(x, a\right. \) und \( f_{a}(x) \) in Metern).
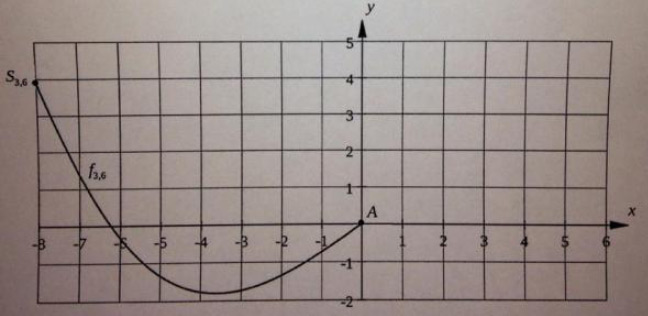
Die Sprungschanzen werden ausgehend vom Startpunkt \( S_{a}\left(-8 \mid f_{a}(-8)\right) \) von links nach rechts durchfahren und so eingebaut, dass der Absprungpunkt \( A(0 \mid 0) \) auf dem Niveau des Erdbodens liegt, das in der Seitenansicht durch die \( x \) -Achse festgelegt ist.
Der Funktionsgraph der Beispielfunktion \( f_{3,6} \) ist in der Abbildung 1 dargestellt.
Aufgabe a:
(1) Weisen Sie nach, dass die durch die Funktion \( f_{a} \) beschriebene Profillinie der Sprungschanze im Bereich \( -\sqrt{3} \cdot a<x<0 \) unterhalb des Niveaus des Erdbodens verläuft.
(2) Bestimmen Sie in Abhängigkeit von a die Koordinaten des tiefsten Punktes \( T_{a} \) des Sprungschanzen-Profils. [Zur Kontrolle: \( \left.T_{a}\left(-a \mid-\frac{1}{2} a\right)\right] \)
(3) Geben Sie eine Gleichung der Funktion kan, auf deren Graph alle Tiefpunkte \( T_{a} \) der Funktionsgraphen von \( f_{a} \) liegen.
Aufgabe b:
Bei der Firma wird eine Sprungschanze bestellt, die im Punkt \( S_{a}\left(-8 \mid f_{0}(-8)\right) \) die Steigung -3 haben soll.
(1) Berechnen Sie den Wert von a, für den die Sprungschanze im Punkt \( S_{a} \) die Steigung
-3 hat, und die Höhe über dem Erdboden, in der sich bei dieser Sprungschanze der Startpunkt \( \mathrm{S}_{\mathrm{a}} \) befindet. [Zur Kontrolle: \( a=\frac{8 \sqrt{5}}{5} \) ]
(2) Laut Angabe der Firma hat die bestellte Sprungschanze zwischen dem Startpunkt \( S_{\text {。 }} \) und dem Absprungpunkt \( A \) die durchschnittliche Steigung \( -\frac{1}{2} \). Prüfen Sie diese Angabe und beurteilen Sie ihre Aussagekraft.
(3) Die bestellte Sprungschanze ist 2 Meter breit. In dem Bereich, in dem ihr Profil unterhalb des Niveaus des Erdbodens verläuft, muss Erde ausgehoben werden. Berechnen Sie, wie groß das Erdvolumen ist, das bis zur Profillinie dieser Sprungschanze ausgehoben werden muss.
Ich brauche e Hilfe bei den Aufgaben a) 1-3 und b) 1-3.