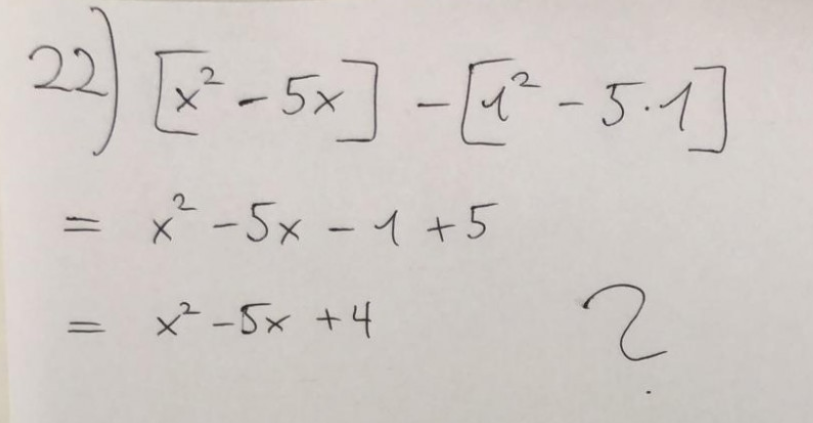Ableitung mit dt und Grenzen

Question

Moin Freunde!

Ich versuche eine Ableitungsaufgabe zu lösen, die ich in dieser Form noch nie gesehen habe. Kann mir hier jemand verraten wie man bei einer solchen Aufgabe vorgeht?

Vielen Dank vorab!

Aufgabe:

\( f(x)=\int \limits_{1}^{x}\left(t^{2}-5 t\right) d t \qquad f^{\prime}(x)=x^{2}-5 x\)

Problem/Ansatz:

Answer 1

Aloha :)

Hier kannst du zuerst integrieren:$$f(x)=\int\limits_1^x\left(t^2-5t\right)dt=\left[\frac{t^3}{3}-\frac{5}{2}t^2\right]_{t=1}^x=\left(\frac{x^3}{3}-\frac{5}{2}x^2\right)-\left(\frac{1}{3}-\frac{5}{2}\right)$$$$f(x)=\frac{x^3}{3}-\frac{5}{2}x^2+\frac{13}{6}$$Und danach ableiten:$$f'(x)=3\cdot\frac{x^2}{3}-2\cdot\frac{5}{2}x=x^2-5x$$

Comments

danke für die Antwort!

Wo kommen nach dem zweiten Gleichzeichen die / 3 und / 2 her?

---

Das Integral von \(t^2\) ist \(\frac{t^3}{3}\) und das Integral von \(5t\) ist \(\frac{5}{2}t^2\).

---

Ahhhh klar stimmt, vielen Dank!!