Hallo Hannah,
Ich verstehe nicht ... wie man erstmal in die Parameterdarstellung kommt...
Nun das geht so: Du hast zwei Punkte \(P\) und \(Q\). Zum Verständnis ist es egal ob wir sie in einer Ebene oder im Raum betrachten. Also hier mal zwei Punkte in der Ebene:
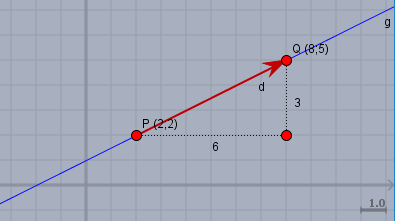
durch die beiden Punkte wird eine Gerade (blau) gelegt. Die Punkte \(P\) und \(Q\) haben im Bild oben die Koordinaten $$P = \begin{pmatrix}2\\ 2\end{pmatrix}, \quad Q = \begin{pmatrix}8\\ 5\end{pmatrix}$$Um die Gerade in Punkt-Richtung-Form zu beschreiben, benötigen wir irgendeinen Punkt auf der Geraden. Es ist wirklich egal welchen - ich wähle \(P\).
Für die Richtung ist es nun notwendig, einen Vektor zu finden, der die Richtung der Geraden beschreibt. Da wir zwei Punkte der Geraden zur Verfügung haben, lässt sich das einfach machen, indem wir die Koordinaten der beiden Punkte von einander abziehen. Unser Richtungsvektor sei \(\vec d\), dann ist$$\vec d = Q - P = \begin{pmatrix}8\\ 5\end{pmatrix} - \begin{pmatrix}2\\ 2\end{pmatrix} = \begin{pmatrix}6\\ 3\end{pmatrix}$$Schau Dir oben im Bild an, was das bedeutet. Der Vektor \(\vec d\) (rot) geht von \(P\) nach \(Q\). Das wäre also ein möglicher Richtungsvektor für die blaue Gerade.
Ich fasse zur Geradengleichung für die Gerade \(g\) zusammen:$$g: \space \vec x = P + t \vec d = \begin{pmatrix}2\\ 2\end{pmatrix} + t \begin{pmatrix}6\\ 3\end{pmatrix}$$Dazu hab ich noch einen sogenannten freien Parameter \(t\) eingefügt. \(t\) kann jetzt jede beliebeige Zahl annehmen. Mit jedem Wert von \(t\) lässt sich nun ein beliebiger Punkt auf der Geraden erreichen. Setze selber mal Werte wie \(0,\, 1,\, 3\) oder \(-1\) in die Geradengleichnug ein und berechne die zugehörigen Punkte und - ganz wichtig(!) - zeichne sie auch in das Koordinatensystem ein.
Bleibt noch zu erwähnen, dass Punkt und Richtung nicht fest gelegt sind. Du kannst zwei beliebige andere Punkte auf der Geraden wählen und das gleiche wie oben noch mal durchführen, um zur Punkt-Richtung-Form zu kommen. Auch darfst Du den Richtungsvektor mit einem beliebigen Wert (\ne 0) multiplizieren. So ist z.B.$$g: \space \vec x = \begin{pmatrix}0\\ 1\end{pmatrix} + s \begin{pmatrix}2\\ 1\end{pmatrix}$$die gleiche Gerade \(g\) wie oben. Warum? Ich habe aber die freie Variable \(s\) genannt, da diese sich nun von dem \(t\) von vorher unterscheidet.
Zur Aufgabe:
wie oben beschrieben, nehme einen der Punkt als 'Stützpunkt' und die Differenz der Vektoren als Richtungsvektor:$$\begin{aligned} g: \space \vec x &= P + t(Q-P) \\&= \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix} + t \left( \begin{pmatrix}10\\ 10\\ -3\end{pmatrix} - \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix}\right) \\ &= \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix} + t \begin{pmatrix}15\\ 21\\ -9\end{pmatrix} && \left| \, \vec d \to \vec d \cdot \frac 13\right.\\& = \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix} + s \begin{pmatrix}5\\ 7\\ -3\end{pmatrix}\end{aligned}$$wie Du siehst habe ich den Richtungsvektor durch 3 geteilt. So bekommt man kleinere Zahlen, mit denen man einfacher rechnen kann.
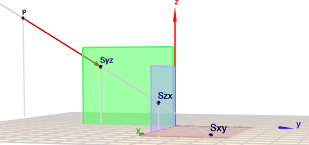
Ein Spurpunkt ist ein Punkt, bei dem eine Koordinate \(=0\) ist. So ist bei allen Punkten in der XY-Ebene die Z-Koordinate \(=0\). Folglich muss \(\vec x (s)\) folgende Gleichung erfüllen$$\vec x(s_{xy}) = \begin{pmatrix}p_x\\ p_y\\ 0\end{pmatrix}$$Nun ist aber \(\vec x\) gleich$$\vec x (s_{s_xy}) = \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix} + s_{xy} \begin{pmatrix}5\\ 7\\ -3\end{pmatrix} = \begin{pmatrix}p_x\\ p_y\\ 0\end{pmatrix}$$In der letzten Koordinatenzeile - also der für die Z-Koordinate steht$$\begin{aligned}6 - 3 s_{xy} &= 0 &&\left| \, -6 \right.\\ -3 s_{xy} &= -6 && \left|\, \div(-3) \right. \\ s_{xy} &= 2\end{aligned}$$Dieses \(s_{xy}=2\) setze nun in die Geradengleichung ein:$$\vec x(s_{xy}=2) = \begin{pmatrix}-5\\ -11\\ 6\end{pmatrix} + 2 \begin{pmatrix}5\\ 7\\ -3\end{pmatrix} = \begin{pmatrix}5\\ 3\\ 0\end{pmatrix}$$Dies ist der Spurpunkt von \(g\) in der XY-Ebene. Auf die gleiche Art und Weise werden nun die anderen beiden Spurpunkte berechnet. Setze einmal die Y-Koordinate und dann die X-Koordinate zu 0. Versuche es mal.
Zum Schluß noch das Bild zur Aufgabe (klick drauf)
Falls noch Fragen offen bleiben, melde Dich bitte.
Gruß Werner