b) der Graph der Funktion \( f(x)=5*(x-2)*(x-4)*(x-t) \) die x-Achse berührt.
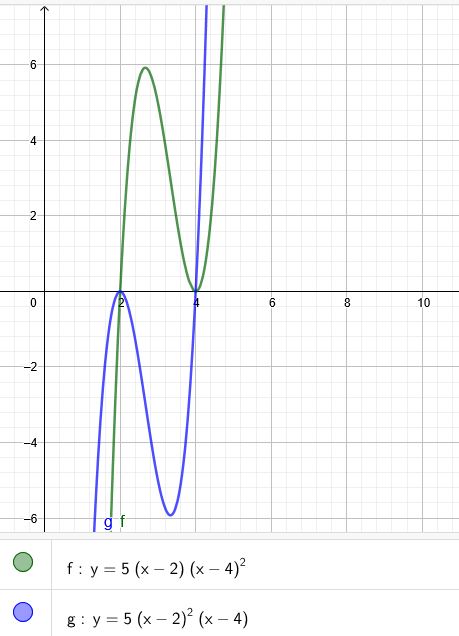
1.)\( f(x)=5*(x-2)*(x-4)*(x-4)=5*(x-2)*(x-4)^2 \) doppelte Nullstelle bei \(x=4\)
2.)\( f(x)=5*(x-2)*(x-4)*(x-2)=5*(x-2)^2*(x-4) \)doppelte Nullstelle bei \(x=2\)
Ohne Substitution und ohne p,q, Formel:
\(x^4-7x^2+10 = 7x^2-8\)
\(x^4-14x^2 = -18\)
\((x^2-\frac{14}{2})^2 = -18+(\frac{14}{2})^2=31 |\sqrt{~~}\)
1.)
\(x^2-\frac{14}{2} = \sqrt{31}\)
\(x^2 = 7+\sqrt{31}\)
\(x₁ = \sqrt{ 7+\sqrt{31}}\)
\(x₂ = -\sqrt{ 7+\sqrt{31}}\)
2.)
\(x^2-\frac{14}{2} = -\sqrt{31}\)
\(x^2 = 7-\sqrt{31}\)
\(x₃ = \sqrt{ 7-\sqrt{31}}\)
\(x₄ = -\sqrt{ 7-\sqrt{31}}\)