Schnittpunkte einer Parabel mit den Koordinatenachsen

Question

Ich bräuchte mal Hilfe bei der folgenden Aufgabe:

"Bestimmen Sie die Schnittpunkte des Graphen der Funktion f mit den Koordinatenachsen.

a) f(x)= x² +6x + 5

b) f(x)= x² +6x - 4

c) f(x)= x² +7x + 4

d) f(x)= x² -6x + 5"

Die Schnittpunkte mit der y-Achse habe ich bereits alle berechnet. Dann habe ich mir gedacht, ich könnte zur Bestimmung der Nullstellen die Werte aus der Formel einfach in die pq-Formel eigeben, also z.B. bei a) -6/2 ± √(-6/2)² +5, aber leider kommen da falsche Zahlen raus... Wenn ich nämlich meinen Taschenrechner den Graphen zeichnen lasse, sind die Nullstellen völlig anders. Wo liegt mein Fehler?

!!

Answer 1

a) -6/2 ± √((-6/2)² -5)

Da muss ein Minus hin. Ergibt sich aus der pq-Formel.

Schaffst Du das dann vollends alleine? Sieht ja sonst gut aus und Ansatz war prinzipiell richtig ;).

Sonst melde Dich nochmals!

Grüße

Comments

Ups, das ist ja fast schon peinlich:DD
Vielleicht hätte ich die Formel doch nochmal nachgucken sollen, anstatt sie so aus meinem Gedächtnis aufzuschreiben...
Vielen Dank auf jeden Fall, jetzt bekomme ich auch die richtigen Lösungen ;)
Schönen Abend noch!

---

Hehe, umso besser, wenn das nun geklärt ist ;).

Gerne und gleichfalls.

Answer 2

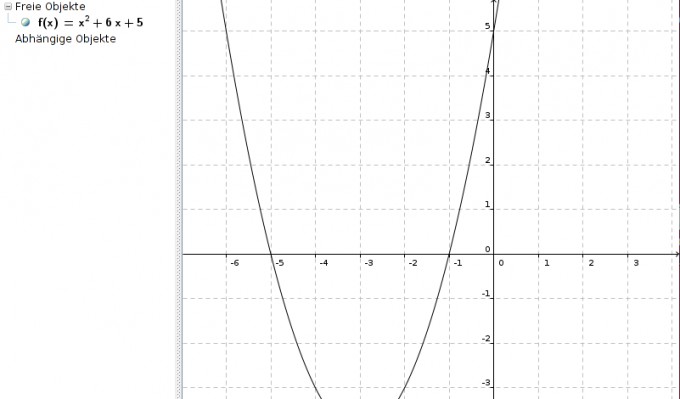
a) f(x)= x² + 6x + 5

Schnittpunkt mit der y-Achse: x = 0 | f(0) = 5 | S(0|5)

Schnittpunkt mit der x-Achse: f(x) = 0 | pq-Formel

x_1,2 = -3 ± √(9 - 5) = -3 ± 2

x₁ = -1 | S(-1|0)

x₂ = -5 | S(-5|0)

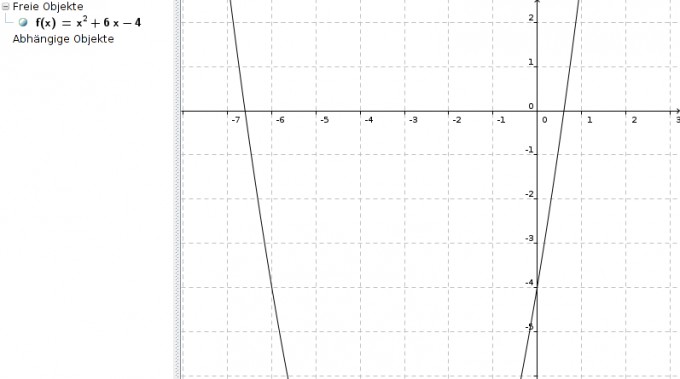
b) f(x)= x² + 6x - 4

Schnittpunkt mit y-Achse: S(0|-4)

Schnittpunkt mit x-Achse:

x² + 6x - 4 = 0

x_1,2 = -3 ± √(9 + 4)

x₁ = -3 + √13 ≈ 0,6056 | S(0,6056|0)

x₂ = -3 - √13 ≈ -6,6056 | S(-6,6056|0)

Die beiden anderen Aufgaben analog :-)

Besten Gruß

Comments

Danke auch an dich für deine Erläuterungen!! Hat mir sehr geholfen:-)

---

Das freut mich sehr!

Und:

Gern geschehen :-)