Berechnen Sie die Schnittpunkte von P mit den Koordinatenachsen.

Question

Aufgabe:

Gegeben ist die Funktion f durch f(x)=2x^2-12x+16. Das Schaubild der Funktion f ist die Parabel P.

a) Berechnen Sie die Schnittpunkte von P mit den Koordinatenachsen.

b) Skizzieren Sie P in einem kartesischen Koordinatensystem.

c) Gegeben ist nun noch die Gerade g durch g(x) = x + 1. Untersuchen Sie rechnerisch die gegenseitige Lage von g und P und berechnen Sie gegebenenfalls die Schnittpunkte von g und P. Skizzieren Sie auch die Gerade in das angelegte Koordinatensystem.

Problem/Ansatz:

Ich weiß leider nicht, wie ich diese Aufgaben lösen soll. Ich würde mich sehr über Erklärungen und Lösungen freuen. Desto mehr es erklärt ist, desto besser. Danke.

Die Scheitelpunkte sind (3/-2), falls diese Information benötigt ist.

Answer 1

f(x) = 2x^2 - 12x + 16

a) Berechnen Sie die Schnittpunkte von P mit den Koordinatenachsen.

Y-Achsenabschnitt

f(0) = 16 → P1(0 | 16)

Nullstellen

2x^2 - 12x + 16 = 0

x = (- b ± √(b^2 - 4ac)) / (2a)

x = 2 ∨ x = 4 → P2(2 | 0) ; P3(4 | 0)

b) Skizzieren Sie P in einem kartesischen Koordinatensystem.

c) Gegeben ist nun noch die Gerade g durch g(x) = x + 1. Untersuchen Sie rechnerisch die gegenseitige Lage von g und P und berechnen Sie gegebenenfalls die Schnittpunkte von g und P. Skizzieren Sie auch die Gerade in das angelegte Koordinatensystem.

Schnittpunkte

f(x) = g(x)

2x^2 - 12x + 16 = x + 1
2x^2 - 13x + 15 = 0

x = (- b ± √(b^2 - 4ac)) / (2a)

x = 1.5 ∨ x = 5

g(1.5) = 2.5 → S1(1.5 | 2.5)
g(5) = 6 → S2(5 | 6)

Answer 2

a) Berechnen Sie die Schnittpunkte von P mit den Koordinatenachsen.

Schnittpunkt mit der y-Achse hat die Koordinaten \((0 | y)\). Einsetzen, ausrechnen, fertig.

Schnittpunkt mit der x-Achse hat die Koordinaten \((x | 0)\). Einsetzen, Gleichung lösen, fertig.

b) Skizzieren Sie P in einem kartesischen Koordinatensystem.

Wertetabelle anlegen, Punkte einzeichnen, Punkte durch eine Kurve verbinden.

berechnen Sie gegebenenfalls die Schnittpunkte von g und P.

Funktionsterme gleichsetzen, Gleichung lösen, Lösung in Funktiongleichung einsetzen.

Skizzieren Sie auch die Gerade in das angelegte Koordinatensystem.

Wertetabelle anlegen, Punkte einzeichnen, Punkte durch eine Kurve verbinden.

Answer 3

Hallo,

\(f(x)=2x^2-12x+16\\ =2(x^2-6x+8)\)

Den Schnittpunkt mit der y-Achse erhältst du, indem du 0 für x in die Gleichung einsetzt.

\(f(0)=2\cdot 0^2-12\cdot 0+16=16\)

Du siehst, du kannst bei diesen Gleichungsformen den Schnittpunkt ablesen, denn der Wert ist die Zahl ohne ein x.

Für die Schnittpunkte mit den Koordinatenachsen = Nullstellen, setzt du die Funktionsgleichung = 0.

Das kannst du beispielsweise mit der pq-Formel machen:

\(2x^2-12x+16=0\\x^2-6x+8=0\\ x_{1,2}=3\pm\sqrt{3^2-8}\\ x_1=3-1=2\quad x_2=3+1=4\)

Du kannst aber auch die Scheitelpunktform verwenden, da der bekannt ist, und die Gleichung nach x auflösen:

\(2(x-3)^2-2=0\quad |+2\\ 2(x-3)^2=2\quad |:2\\ (x-3)^2=1\quad \sqrt{}\\ x-3=1\Rightarrow x = 4\\ x-3=-1\Rightarrow x = 2\)

Der Graph sieht so aus:

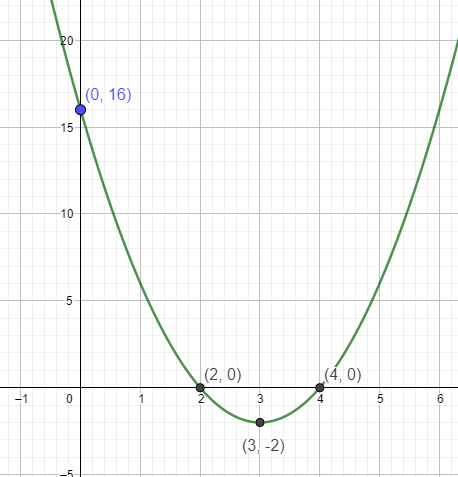
Um festzustellen, ob zwei Graphen sich schneiden, setzt du die Funktionsgleichungen gleich.

\(2x^2-12x+16=x+1\\ 2x^2-13x+15=0\\ x^2-6,5x+7,5=0\\ x_{1,2}=3,25\pm\sqrt{3,25^2-7,5}\\ x_1=1,5\quad x_2=5\)

Um die y-Koordinaten der Schnittpunkte zu berechnen, setzt du die Ergebnisse in g(x) ein. Du kannst sie natürlich auch in f einsetzen, wenn du gerne rechnest ;-)

Graphisch sieht das so aus:

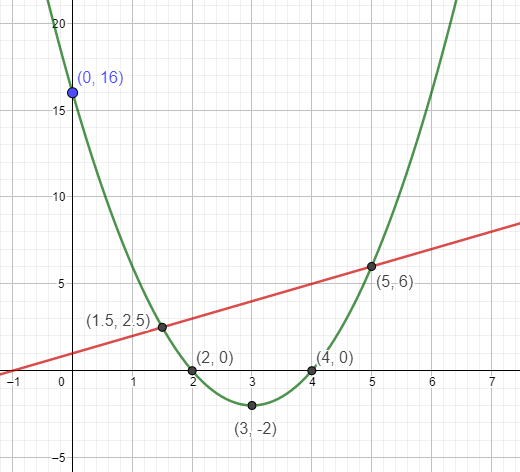
Melde dich, falls du noch Fragen hast.

Gruß, Silvia