Hallo,
schau Dir folgendes Rechteck an.
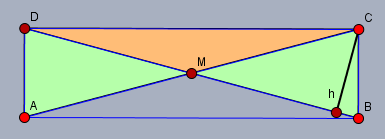
Die Diagonalen halbieren einander, d.h. \(|DM|=|MB|\) und \(|AM|=|MC|\). Damit sind die gegenüberliegenden Dreiecke (grün) gleich und somit auch gleich groß. Es ist$$F_{AMD} = F_ {MBC}, \quad F_{ABM} = F_{CDM}$$ Die Dreiecke \(\triangle DMC\) (hellbraun) und \(\triangle MBC\) haben die gemeinsame Höhe \(h\) über der Grundseite \(DM\) bzw. \(MB\). Aus der Gleichheit der beiden Grundseiten folgt die Gleichheit der Flächen$$F_{DMC} = \frac 12 h |DM| = \frac 12 h |MB| = F_{MBC}$$Also haben alle vier Dreiecke den gleichen Flächeninhalt.
Das gilt für Parallelogramme in gleicher Weise.