Aufgabe:
Wir betrachten den affinen Raum \( (A, V,+) \) für \( A=V=\mathbb{R}^{3} \) und
+ die übliche Addition von Vektoren und Punkten im \( \mathbb{R}^{3} \). Weiter seien die Abbildungen Translation \( t_{v}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) und für \( \lambda \neq 0 \) die zentrische Streckung \( s_{Z}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) mit
$$ t_{v}(P):=P+v $$
und
$$ s_{Z}(P):=Z+\lambda \cdot \overrightarrow{Z P} $$
gegeben, die Sie in der Vorlesung als Beispiele für bijektive affine Abbildungen kennen gelernt haben. Wir betrachten das von den Einheitsvektoren \( e_{1}, e_{2}, e_{3} \in \mathbb{R}^{3} \) und dem Nullpunkt (0,0,0)\( \in A \) aufgespannte Polygon
$$ \mathbb{P}:=\left\{(0,0,0)+\alpha e_{1}+\beta e_{2}+\gamma e_{3}, \alpha+\beta+\gamma \in[0,1]\right\} \subset A $$
Nachfolgend sind Bilder von \( \mathbb{P} \) unter den Abbildungen \( t_{v} \) und \( s_{Z} \) für spezifische Werte \( v, \lambda, Z \) gegeben. Beschreiben Sie mathematisch nachvollziehbar, wie die konkreten Abbildungen \( \mathbb{P} \) verändern und skizzieren Sie die Bilder.
a) \( t_{v}(\mathbb{P}) \) für \( v=\left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right) \)
b) \( s_{Z}(\mathbb{P}) \) für \( \lambda=2 \) und \( Z=(0,1,0) \)
c) \( \left(s_{Z} \circ t_{v}\right)(\mathbb{P}) \) für \( \lambda=-1, Z=(0.5,0.5,0.5) \) und \( v=(0,0,1) \)
Ansatz
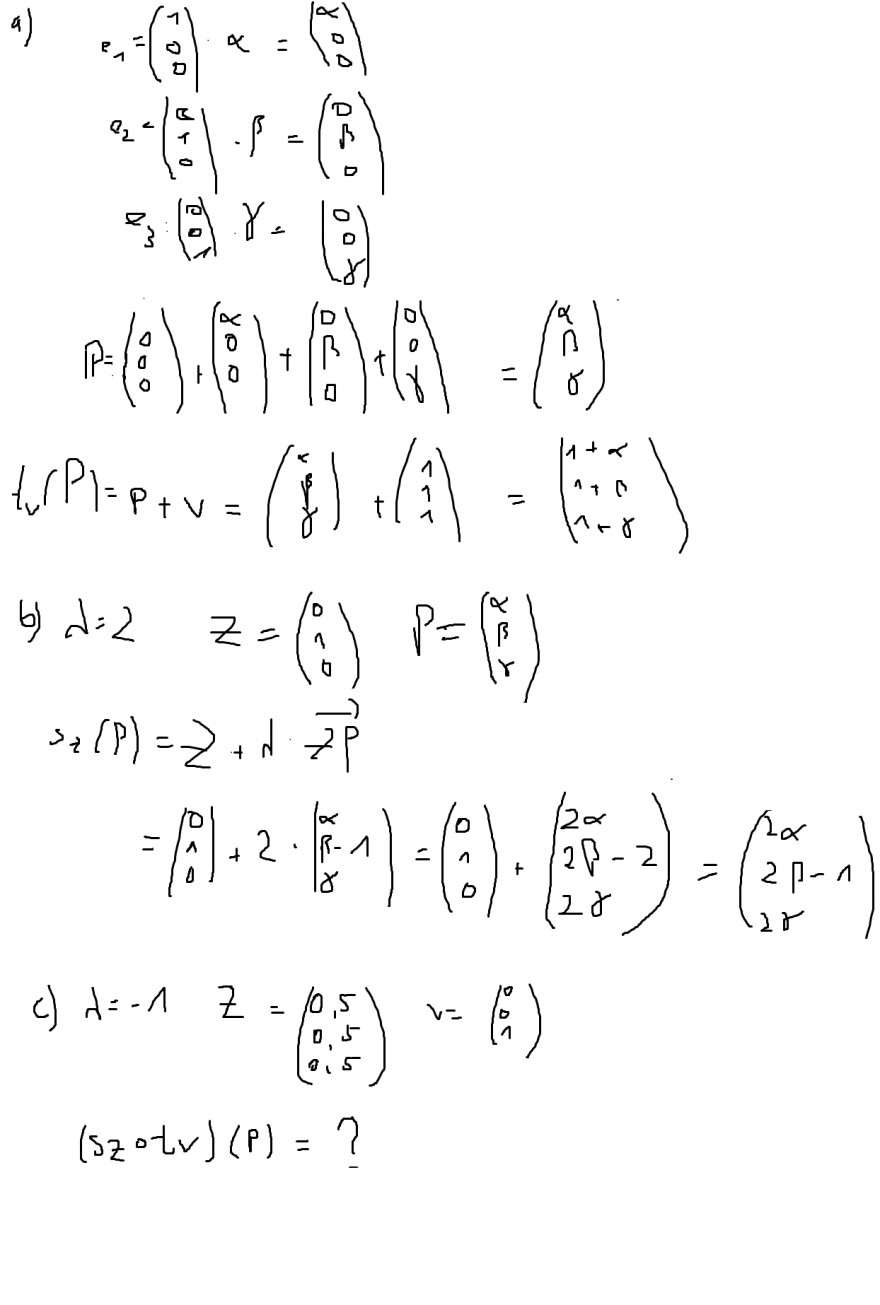
Ich bin mir nicht sicher, ob das korrekt ist.
bei c) weiß ich nicht wirklich, wie ich das machen soll.
Wie skizziere ich vor allem die Bilder?