Extremwertaufgabe: Eine trapezförmige Rinne aus einem Brett der Breite 10 cm, soll...

Question

Aufgabe 8 (Optimierung):

Problemstellung: Eine trapezförmige Rinne aus einem Brett der Breite 10 cm, welches in der Waagerechten liegen soll und zwei weiteren Brettern der Breite 10 cm soll einen möglichst großen Querschnitt haben. Wie müssen die Bretter angeordnet sein?

Machen Sie zunächst eine Skizze und stellen dann eine zu maximierende Funktion in einer Variablen auf.

Aufgabe 9 (Optimierung):

Berechnen Siedie Lösung aus Aufgabe 8, indem Sie:

a) die in Aufgabe 8 erhaltene Funktion ableiten.

b) die Nullstellen(n) der Ableitung bestimmen.

c) die Ränder untersuchen.

Answer 1

Hallo Jürgen,

 

das Ganze soll wohl in etwa so aussehen:

 

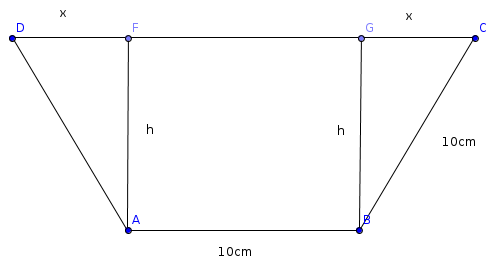
Die Fläche des Trapezes, also der Querschnitt der Rinne ist dann

A = (10 + 10 + 2x)/2 * h

h² + x² = 10² = 100

Wir lösen nach h auf:

h² = 100 - x²

h = √(100 - x²)

Dann ist die Fläche des Trapezes eine Funktion von x:

f(x) = (20 + 2x)/2 * √(100 - x²)

f(x) = (10 + x) * √(100 - x²)

Produktregel

(uv)' = u'v + uv'

u = 10 + x

u' = 1

v = √(100 - x²) = (100 - x²)^1/2

Kettenregel

Innere Ableitung = -2x

Äußere Ableitung = 1/2 * (100 - x²)^-1/2 = 1/[2 * √(100 - x²)]

v' = -2x * 1/[2 * √(100 - x²)] = -x / √(100 - x²)

Insgesamt:

f'(x) = (100 - x²)^1/2 - (10 + x) * x * (100 - x²)^-1/2

f'(x) = 0

(100 - x²)^1/2 = (10 + x) * x * (100 - x²)^-1/2 | : (100 - x²)^-1/2

100 - x² = 10x + x² | -10x - x²

100 - 10x - x² - x² = 0

-2x² - 10x + 100 = 0 | :(-2)

x² + 5x - 50 = 0

pq-Formel

x_1,2 = -5/2 ± √(25/4 + 200/4) = -5/2 ± 15/2

x₁ = 10/2 = 5

x₂ = -20/2 = -10

 

Die negative Lösung ist im Sachzusammenhang unsinnig, also muss gelten:

x = 5cm

 

x² + h² = 100

25 + h² = 100

h² = 75

h = √75

 

Dann hat das Trapez die Fläche

(10 + 10 + 2x)/2 * h =

15 * √75 ≈

129,90 (cm²)

 

Hoffentlich habe ich mich nicht verrechnet :-D

 

Besten Gruß und viel Erfolg für morgen

Answer 2

hi

 

flächeninhalt trapez:
A = (a+c)h/2
soll maximal werden

A(x) = (a + c(x))h(x)/2

c(x) = a + 2x
h(x) = √(b² - x²)
c(x) und h(x) einsetzen in A(x)

A(x) = (a + a + 2x)*√(b² - x²)/2
A(x) = (2a + 2x)*√(b² - x²)/2
A(x) = (a + x)*√(b² - x²)/2
A(x) = (10 + x)*√(100 - x²)/2

a: breite des bretts
b: breite des bretts
es gilt a = b = 10cm

a)
A'(x) = -(2*(x^2 + 5x - 50))/sqrt(100-x^2)

b)
-(2*(x^2 + 5x - 50))/sqrt(100-x^2) = 0
-> x = 5

bei x = 5 bekommen wir
c = a + 2*5
c = 20
und
h = √(100 - 25)
h = 8,66 gerundet

das ergibt einen flächeninhalt von
A = (a+c)h/2  = (10 + 20)*8,66 /2
A = 129,9 cm² gerundet

c)
?