Wie stelle ich die Nebenbedingungen der Extremalaufgabe (Trapez) heraus?

Question

Aufgabe:

Extremalaufgaben Trapez mit Funktion

Problem/Ansatz:

Hallo, ich brauche Hilfe für das Lösen dieser Extremalaufgabe.

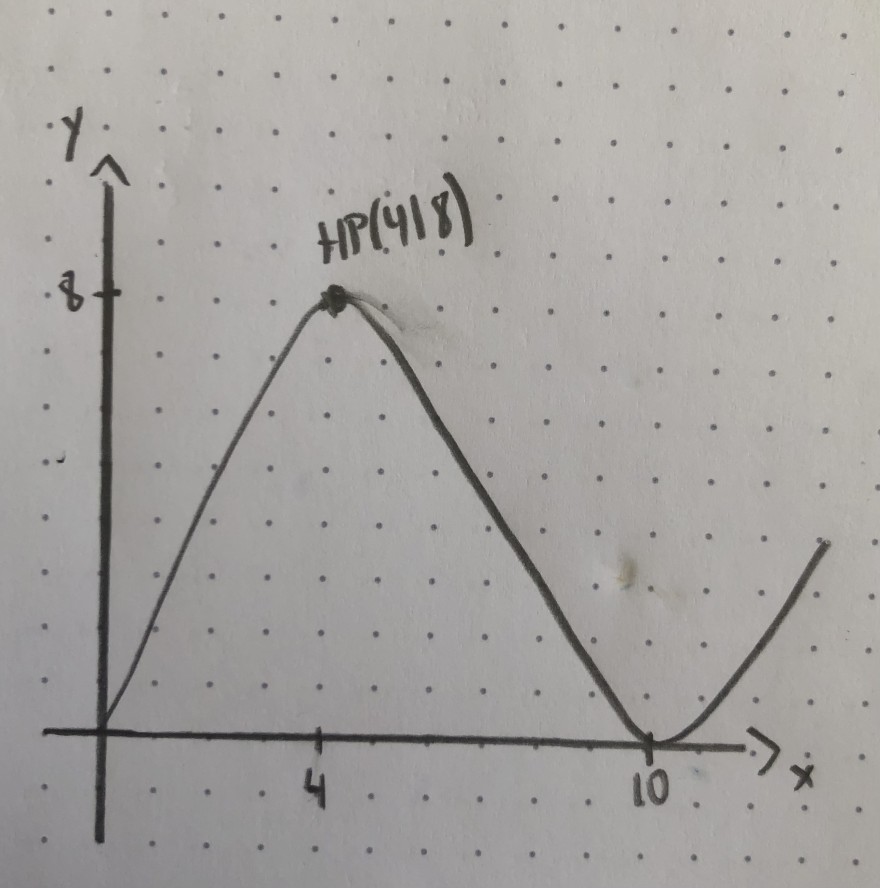
Und zwar müssen wir den maximalen Flächeninhaltes eines Trapez ermitteln, hierfür ist die Funktion des Graphen gegeben {f(x)=1/36x^3-13/18x^2+40/9x}. Außerdem muss die Grundseite des Trapezes vom Ursprung zu dem Punkt (8|0) gehen. Zudem sollen die jeweils zwei anderen Punkte, die dann die Strecke c ergeben, auf der f(x) liegen.

Die Hauptbedingung habe ich schon:

Hb:  A=(a+c)/2 • h

Allerdings tue ich es mir schwer die Nebenbedingungen aufzustellen.

Nb: a=8    h= f(x)

Aber wie kriege ich die Strecke c heraus?

Comments

\(f(x)=\frac{1}{36}x^3-\frac{13}{18}x^2+\frac{40}{9}x\)  sieht so aus:

---

ich glaube, du hast die f(x) falsch eingegeben. Bei Geogebra sieht sie nämlich so aus:

---

So steht es bei dir: {f(x)=1/36x^3-13/18x^2+40/9x}.

Bei deiner GeoGebra Zeichnung fehlt das x bei 40/9

---

Du hast Recht : Ich hatte einen falschen Bruch dabei.

Answer 1

Hier eine etwas bessere Skizze zum Problem:

Die Berechnung von x₂ - x₁ in Abhängigkeit von h schafft nicht einmal mein CAS so, dass man das verwenden lönnte.

Comments

Das mit x1-x2 habe ich mir auch schon gedacht, aber ich weiß nicht, wie ich es als Nebenbedingungen aufschreiben soll bzw. was dann die Zielfunktion wäre

---

Angenommen x₂ - x₁ in Abhängigkeit von h sei berechenbar, dann lautet die Zielfunktion Z(h)=h·(x₂-x₁+8)/2.

---

Das heißt ausgeschrieben, hieße es dann A= (1/36x^3-13/18x^2+40/90x)•(x2-x1+8)/2 ?

---

Nein. x₁ und x₂ sind zwei Lösungen der Gleichung h=1/36x³-13/18x²+40/9x. Das Problem ist, diese Lösungen und deren Differenz zu bestimmen.

---

ahh…und wissen Sie, wie man das tut? Weil ich steh im Moment sehr auf dem Schlauch, wie ich an so etwas weiter angehen sollte

---

Ich hatte zunächst gehofft, dass mir Computer-Algebra (CAS) helfen würde. Aber selbst da wurde es sehr kompliziert. Mag aber sein, dass es mit CAS geht.

---

Die Berechnung von x2 - x1 in Abhängigkeit von h schafft nicht einmal mein CAS

Dann mach es anders herum.

---

Wie gewohnt: kryptisch. kryptisch, kryptisch. Ich weiß, dass du jeden dazu animieren möchtest, sein Gehirn einzuschalten - aber mein Gehirn kann dir manchmal nicht folgen.

---

Diesmal war es nun absolut nicht kryptisch : Du sollst nicht c in Abhängigkeit von h bestimmen sondern c als unabhängige Variable nehmen und h in Abhängigkeit von c ausdrücken.
Zwischenergebnisse : Ein zu c gehöriger x-Wert ist x(c) = c/2+26/3 - √(196/9-c^2/12),
h=f(x(c))  und A(c) = (4+c/2)*f(x(c))

---

Jetzt hab ich es verstanden - vielen Dank. Bleibt die Hoffnung, dass auch gaaaaaaast67 verstanden hat.

---

Die Aufgabe erscheint mir für eine Schulaufgabe viel zu schwer.

@gaaaaaaast67: woher stammt die Aufgabe?

Meines Erachtens ist das nur nummerisch zu lösen. Wolfram Alpha kommt auf ein Maximum bei \(x_1\approx 2,453\) (nummerisch). In Desmos lässt sich prüfen, ob das sinnvoll ist (verschiebe den lila Punkt):

---

Vielen Dank, jetzt hab ich es verstanden! Die Aufgabe sollen wir für meinem Mathe Lk lösen.

Answer 2

Vielleicht wäre es eine Möglichkeit, ein maximales Rechteck einzubeschreiben; dann ist das Trapez ja auch maximal.

Comments

Vielleicht wäre es eine Möglichkeit, ein maximales Rechteck einzubeschreiben; dann ist das Trapez ja auch maximal.

Wie meinst du das?

Es ist doch ein typisches Trapez gesucht, nicht dessen Spezialfälle.

Intuitiv würde ich sagen, dass es größere "Normal-Trapeze" gibt als

Rechtecke, weil man die Basis über die Rechteckbasis hinaus verlängern kann

bei gleicher Breite/Höhe. Siehe Bild von Roland.

Ferner wäre sonst wohl explizit von einem Rechteck die Rede.

Answer 3

Hallo,

ein Anfang ...

Nach einiger Arbeit:

Comments

Das wäre tatsächlich ein Anfang, aber ich weiß nicht ganz wie ich daraus eine hb oder nb herausfinden kann.

---

Ich habe zuerst eine Ursprungsgerade g(x)=m•x gezeichnet. Dabei liegt m zwischen 2 und 40/9.

Den Schnittpunkt für 0<x<4 kann man in Abhängigkeit von m ausrechnen.

x1=13-√(9+36m), y1=m•x1=y2=h

Jetzt müsste noch x2 ermittelt werden, indem man f(x2)=h setzt.

Ich sehe aber gerade, dass sich in den Kommentaren zu Rolands Antwort ein anderer Ansatz verbirgt.