Hallo,
im Allgemeinen ist es sinnvoll, zuerst das \(\lambda\) zu entfernen, indem man eine der beiden Ableitungen nach \(x\) oder \(y\) nach \(\lambda\) auflöst und in die jeweils andere einsetzt. $$\begin{aligned} L(x,y,λ) & =- \frac 12(x^2+y^2)+1000-λ(300-x^2-y^2-xy) \\ \frac{\partial L}{\partial x} &= -x + \lambda (2x + y) = 0 \implies \lambda = \frac{x}{2x+y}\\ \frac{\partial L}{\partial y} &= -y + \lambda(2y + x )= 0 \\ y &= \frac{x}{2x+y} \cdot (2y + x ) \\ 2xy + y^2 &= 2xy + x^2 \\ \implies x_{1,2} &= \pm y\\ \end{aligned}$$und das setzt man nun in die Nebenbedingung ein:$$\begin{aligned} x^2+y^2+xy &= 300 \\ 2y^2 \pm y^2 &= 300 \\ \implies y_{1,2} &= \pm 10, \quad y_{3,4} = \pm 10 \cdot \sqrt 3 \end{aligned}$$
Das sind die Minima bei \(\pm(10 \sqrt 3; \, -10 \sqrt 3)\)
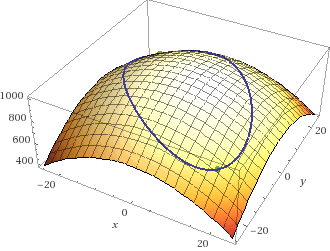
und die Maxima bei \(\pm (10;\, 10)\):
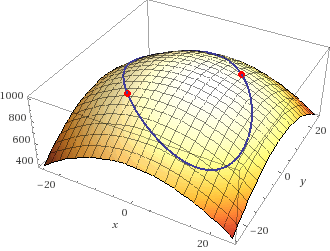
Die blaue Ellipse, die auf dem Paraboloiden liegt, ist die Nebenbedingung.