Es seien X_{1} und X_{2} Zufallsgrößen. Berechnen Sie Cov(12 X_{1} - X_{2}, X_{1} - 8X_{2})

Question

Aufgabe:

Es seien \( X_{1} \) und \( X_{2} \) Zufallsgrößen mit \( \sigma_{1}^{2}=2, \sigma_{2}^{2}=13 \) und \( \operatorname{Cov}\left(X_{1}, X_{2}\right)=\sigma_{12}=-2 \)

Berechnen Sie \( \operatorname{Cov}\left(12 X_{1}-X_{2}, X_{1}-8 X_{2}\right) \)

322.0

Kann mir bitte jemand helfen wie man das z.B. in wolframalpha eingibt?

Answer 1

Aloha :)

Du kannst die Kovarianz einfach ausmultiplizieren, ähnlich wie beim Distributivgesetz:$$\operatorname{cov}(12X_1-X_2,X_1-8X_2)$$$$=12\operatorname{cov}(X_1,X_1)-\operatorname{cov}(X_2,X_1)-12\cdot8\operatorname{cov}(X_1,X_2)+8\operatorname{cov}(X_2,X_2)$$$$=12\sigma_1^2-97\sigma_{12}+8\sigma_2^2$$$$=12\cdot2-97\cdot(-2)+8\cdot13$$$$=322$$

Comments

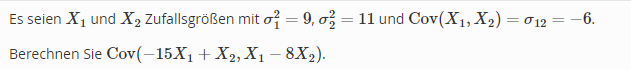
Text erkannt:

Es seien \( X_{1} \) und \( X_{2} \) Zufallsgrößen mit \( \sigma_{1}^{2}=9, \sigma_{2}^{2}=11 \) und \( \operatorname{Cov}\left(X_{1}, X_{2}\right)=\sigma_{12}=-6 \).
Berechnen Sie \( \operatorname{Cov}\left(-15 X_{1}+X_{2}, X_{1}-8 X_{2}\right) \).

hier komme ich nicht weiter. Wenn ich ausklammere, komme ich auf

-15*cov(x,x) + cov(x,y)-8*cov(y,x) + 8*cov(y,y), das ist aber falsch...

---

\((-15)\) mal \((-8)\) ist \(120\):$$\phantom=-15\operatorname{Cov}(X_1;X_1)+\operatorname{Cov}(X_1;X_2)+120\operatorname{Cov}(X_1;X_2)-8\operatorname{Cov}(X_2;X_2)$$$$=-15\operatorname{Var}(X_1)+121\operatorname{Cov}(X_1;X_2)-8\operatorname{Var}(X_2)$$

---

Vielen Dank, aber warum hinten -8var(y) und nicht +?

---

Weil \(1\) cdot \((-8)\) gleich \((-8)\) ist.

---

Danke dir! Habe es verstanden