Bernoulli Formel richtig anwenden und Grenzwert berechnen

Question

Aufgabe:

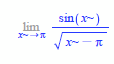
Text erkannt:

\( \lim \limits_{x \rightarrow \pi} \frac{\sin (x)}{\sqrt{x \sim-\pi}} \)

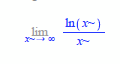
Text erkannt:

\( \lim \limits_{x \rightarrow \infty} \frac{\ln (x)}{x} \)

Grenzwert mit Hilfe von Bernoulli bestimmen.

Problem/Ansatz:

1.Aufgabe:

x~ = x > pi

ich habe  0/0, wenn pi eingesetzt

Ableitung sin(x~) -> cos(x~)

Ableitung Wurzel(x~ - pi) -> 1/2√x−π

-> Grenzwert pi einsetzen = 1/0  Lösung wäre = 0, was mache ich falsch?

2. Aufgabe:

x~= x > 0

Grenzwert eingesetzt = unendlich/unendlich

Ableitung : ln(x~) -> 1/x~

Ableitung : x~ = 1

1/x~ -> 1/unendlich = 0

Stimmt diese zweite Berechnung und was mache ich bei der ersten falsch?

Liebe Grüsse

Comments

Dein  meinst den L'Hospital, oder?

Was bedeuten die Tilden bei x?

---

Hallo,

die Regel heißt Bernoulli-lhospital.

Du schreibst immer Aufleitung, aber es heißt Ableitung!

Zur zweiten Aufgabe!

lim x--->oo ln(x)/x = lim x-->oo (1/x )/1 =0

Das hast du richtig gerechnet.

Bei der ersten Aufgabe hast du die Wurzel falsch abgeleitet!

---

Sorry, ich meine natürlich die Ableitung! Falsch geschrieben!

Bei mir in der Aufgabe steht andauernd x~ dies wäre sozusagen das x-, passe ich kurz an. Und ich leite mal die Wurzel nochmal ab. Danke.

---

...was mache ich bei der ersten falsch?

Es ist $$\left(\sqrt{x}\right)^{\prime}=\dfrac{1}{2\cdot\sqrt{x}}$$

---

Ich bekomme für die Ableitung: 1/2√x−π -> Wenn ich den Grenzwert pi einsetze, bekomme ich ja 1/0 und dies funktioniert nicht..

x~ > Pi (Damit diese reell ist)

Muss ich dabei etwas beachten?

---

x~ > Pi (Damit diese reell ist)

Was soll das heißen und wozu dient die Tilde?

Muss ich dabei etwas beachten?

Ja, die Quadratwurzelfunktion ist an der Stelle 0  nicht differenzierbar.

---

In der Aufgabe steht x~

und x~  ist definiert als x > pi

---

Ich verzichte auf die Tilde, denn es ist ohnehin klar, dass wir uns im Definitionsbereich des Terms bewegen müssen. Meine Rechnung: $$\lim\limits_{x\to\pi}\dfrac{\sin(x)}{\sqrt{x-\pi}} = \lim\limits_{x\to\pi}\dfrac{\cos(x)}{\dfrac{1}{2\cdot\sqrt{x-\pi}}} = 2\cdot\lim\limits_{x\to\pi} \left(\sqrt{x-\pi}\cdot\cos(x)\right)=\dots$$