Bestimmen Sie den Typ der Quadrik Q.

Question

Betrachten Sie die von einem Parameter alpha € R abhängige Quadrik
Q_a :={ x element R I -x_1^(2)-x_2^(2)-alphax_3^(2)-6x_1x_2 -4x_1+4x_2-2alphax_3-alpha = 0}
(a) Schreiben Sie die Gleichung der Quadrik Q_a. in Matrixform.
(b) Bestimmen Sie den Typ der Quadrik Q_a. in Abhängigkeit von a.
(c) Bestimmen Sie eine euklidische Normalform von Q_a. in Abhängigkeit von a.
(d) Geben Sie die Gestalt von dieser Quadrik in Abhängigkeit von n, an.

Könnt ihr mir bitte ausführlich mit rechenschritt erklären?

Vielen Dank

Comments

Ist \(-x^2-y^2-\alpha z^2-6xy-4x+4y-2\alpha z-\alpha=0\)  gemeint?
Dann ist das äquivalent zu \(-(x+3y+2)^2+8(y+1)^2-\alpha(z+1)^2=4\).

---

-x₁²-x₂²+αx₃²-6x₁x₂-4x₁+4x₂-2αx₃-α = 0

so ist das richtig.

---

Bitte mit dem rechenschritten dazu :)

---

ich komme nicht weiter :(

Answer 1

Ich würde mir das erstmal anschauen z.B. in GeoGebra....

zweckslesbakeit

-x²-y²+αz²-6xy-4x+4y-2αz=α

===> \(\small A \, :=  \, \left(\begin{array}{rrr}-1&-3&0\\-3&-1&0\\0&0&\alpha\\\end{array}\right) , a^T \, :=  \, \left\{ -4, 4, 2 \; \alpha \right\} , a_0 \, :=  \, \alpha\)

JD:=JordanDiagonalization(A) ===>

\(\small JD \, :=  \, \left\{ \left(\begin{array}{rrr}-1&1&0\\1&1&0\\0&0&1\\\end{array}\right), \left(\begin{array}{rrr}2&0&0\\0&-4&0\\0&0&\alpha\\\end{array}\right) \right\} \)

===> Drehung/Rotation R

\(\small R \, :=  \, \left(\begin{array}{rrr}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\0&0&1\\\end{array}\right)\)

q_D(X):=(x,y,z) D (x,y,z) + a R (x,y,z) =  α

\(q_D: \, \alpha \; z^{2} + 2 \; x^{2} - 4 \; y^{2} + 2 \; \alpha \; z - 4 \; \sqrt{2} \; x = \alpha\)

Translation

\(T \, :=  \, \left\{ x = x + \sqrt{2}, y = y, z = z - 1\right\} \)

q_D(T)

\(q_N: \, \alpha \; z^{2} + 2 \; x^{2} - 4 \; y^{2} = 2 \; \alpha + 4\)

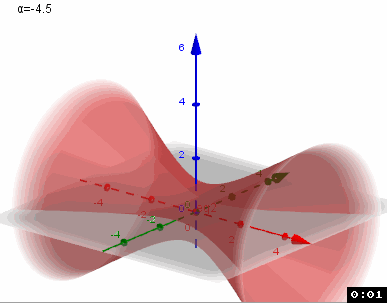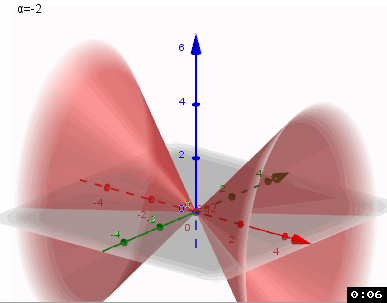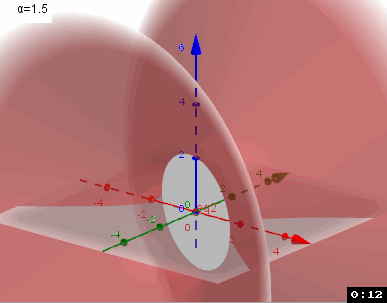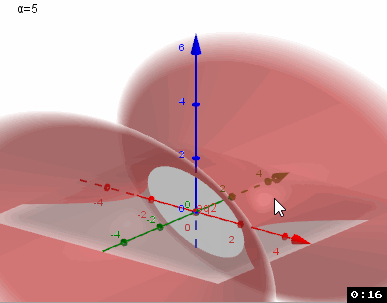
Kommst Du nun zurecht?

Comments

ist das ein beispiel aufgabe?

iich komme leider doch nicht so recht

---

ich verstehe auch die rechenschritte nicht.

wie kommt bzw. wie rechnet man das.

---

Ich hab Deine Aufgabe bis zur (euklidschen) Normalform durchgerechnet, eine Hauptachsentransformation sollte doch bekannt sein, wenn Du an solche Fragestellungen herangehst?

Wenn Du nicht zurecht kommt mußt Du konkrete Fragen stellen was wo unklar ist...

---

also

wie errstelle ich die Matrix form.

und bei deinem beispiel sehe ich nur andere zahlen.

was wichtiger für mich aber ist, das ich die rechenschritte nachvollziehen kann.

---

Ja, finde ich auch....

Welche Zahlen sind anders - ich habe Deine Aufgabe übernommen

---

ah k

aber habe ich den salat^^

-x²-y²+αz²-6xy-4x+4y-2αz=α

===> A:=⎛⎝⎜−1−30−3−1000α⎞⎠⎟

das zitiren hat irgwie nicht geklappt.

wie kommst du von dieser Gleichung auf

diese matrix?

also wie muss man vorgehen.

---

A (a_ij) entsteht durch Übertragen der quadratischen Koeffizienten x_i² in die Diagonale a_ii und die gemischten/2  x_ix_j auf a_ij - das ist das kleine EinmalEins der Hauptachsentransformation - wie bist Du bisher damit verfahren?

---

ich muss das ganze noch einmal üben.

was fehlt den gerade noch?

---

Hm,

Deine Übungen kannst Du mit der App

https://www.geogebra.org/m/pempffkx

überprüfen...

Die Fälle Deiner Quadrik betreffen

α<-2, α=-2, -2<α<0, α=0, α>0

Anschauung: Kopiere die Normalform oder

-x^(2)-y^(2)+α z^(2)-6 x y-4 x+4 y-2 α z=α

nach https://www.geogebra.org/classic#3d

α wird als Schieberegler eingetragen und kann die Änderungen im 3D-Fenster darstellen....

---

vielen Dank für deine mühen :)