Hallo Karen,
Zeichne das ganze zunächst in der YZ-Ebene auf:
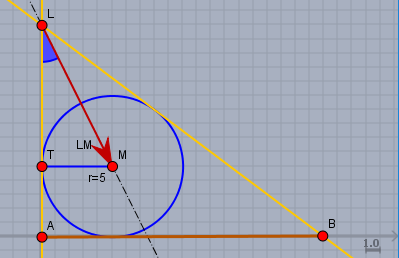
Die beiden Strahlen, die von der Lichtquelle \(L\) ausgehen, bilden den Lichtkegel um die Kugel (blau). Der Schatten in der XY-Ebene ist hier als die braune Strecke \(AB\) angedeutet. In dieser Perspektive ist die XY-Ebene nur ein Strich.
Der halbe Öffnungswinkel \(\alpha = \angle TLM\) berechnet sich aus dem rechtwinkligen Dreieck \(\triangle TML\). Es ist $$\cos \alpha = \frac{|LT|}{|LM|} = \frac{10}{5 \sqrt 5} = \frac 25 \sqrt 5 \implies \alpha \approx 26,6°$$Um die Form des Schattens zu berechnen betrachtet man den Vektor \(\vec{LP}\), der von der Lichtquelle \(L\) zu einem beliebigen Punkt auf der Schattengrenze in der XY-Ebene verläuft. Da \(P\) sich auf dem Lichtkegel befindet, ist der Winkel zwischen dem Vektor \(\vec{LM}\) und \(\vec{LP}\) immer \(= \alpha\). Das Skalarprodukt beider Vektoren ist folglich $$\left< \vec{LP}, \vec {LM} \right> = |\vec{LP}| \cdot \underbrace{|\vec{LM}| \cdot \cos \alpha }_{= |LT| = 10}$$Und der Vektor \(\vec{LP}\) ist$$\vec{LP} = P - L = \begin{pmatrix} x\\y\\ 0 \end{pmatrix} - \begin{pmatrix} 0\\ 0\\15 \end{pmatrix} = \begin{pmatrix} x\\y\\ -15 \end{pmatrix}$$Einsetzen in die Gleichung vom Skalarprodukt und auflösen gibt:$$\begin{aligned} 5y + 150 &= 10 \sqrt{x^2+y^2 + 225} \\ y + 30 &= 2 \sqrt{x^2+y^2 + 225} \\ y^2 + 60 y + 900 &= 4x^2 + 4y^2 + 900 \\ 4x^2 + 3y^2 - 60 y &= 0\\ 4x^2 + 3(y^2 - 20 y + 100) &= 300\\ 4x^2 + 3(y - 10)^2 &= 300\\ \frac {x^2}{(5 \sqrt 3)^2} + \frac{(y-10)^2}{10^2} &= 1 \end{aligned}$$Der Schatten ist also eine Ellipse mit Mittelpunkt bei \((0;10)\), großer Halbachse \(b=10\) in Y-Richtung und kleiner Halbachse \(a=5\sqrt 3\) in X-Richtung.
Und hier noch ein Versuch, das ganze in 3D darzustellen (Maßstab 1:2).
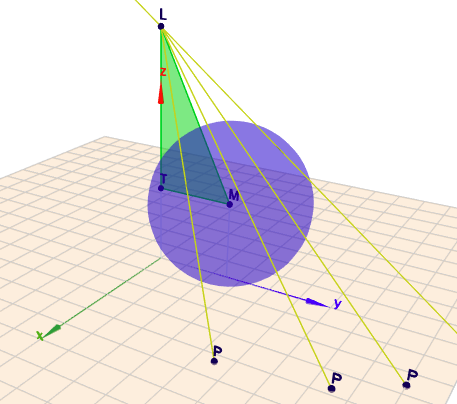
Geoknecht3D kann leider keine Ellipsen. (klick auf das Bild)