Parabel Frage: Gelingt es der Golferin, das Hindernis "Baum" in 120 m Entfernung zu überspielen?

Question

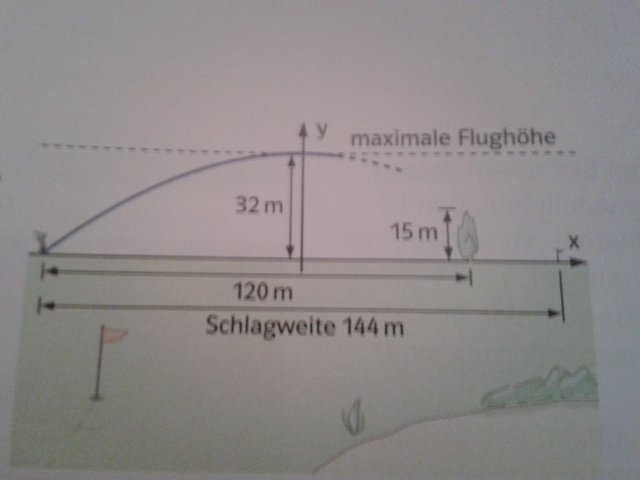
1. Realsituation:

Gelingt es der Golferin, das Hindernis Baum in 120 m Entfernung zu überspielen?

2. Mathematisches Modell:

Die Fugkurve eines Golfballs lässt sich mit einer Parabel modellieren. Hier ist es günstig, den Ursprung des Koordinatensystems auf Höhe 0 m senkrecht unterhalb des Scheitels zu legen.

Allgemeine Parabelgleichung:
\( f(x)=-a \cdot x^{2}+c \)

Durch Einsetzen der Zahlenwerte erhält man:
\( 0=-a \cdot 72^{2}+32 \)
\( a=\frac{32}{72^{2}}=\frac{1}{162} \)
\( f(x)=-\frac{1}{162} x^{2}+32 \)

3. Mathematisches Ergebnis:

\( f_{8}(x)=-\frac{1}{162} \cdot 48^{2}+32=17,8 \)

4. Reales Ergebnis:

Im Idealfall fliegt der Ball etwa \( 2,8 \mathrm{m} \) über den Baumwipfel hinweg.

Problem:

Das ist eine Beispielaufgabe die in meinem Mathebuch vorgegeben ist. Ich verstehe den Schritt nicht wo auf einmal aus 0 = -a·72² + 32 ein a = 32/72² = 1/162 wird. Müsste da nicht a=72²+32 sein? Warum geteilt? Und woher kommt aufeinmal 1/162?

Answer 1

0 = - a * 72² + 32

Hier kannst du nicht einfach plus a rechnen, denn das - a ist ja Faktor eines Produktes. Einen Faktor aber kann man nicht einfach "wegaddieren".

Statt dessen musst du auf beiden Seiten a * 72 ² addieren und erhältst:

<=> a * 72 ² = 32

Nun musst du beide Seiten durch 72 ² dividieren. Es ergibt sich:

<=> a = 32 / 72 ²

und das ist genau die Gleichung, die auch in deinem Buch steht.

Comments

Achso ich verstehe Danke :DD aber ich habe nicht auf beiden seiten +a gemacht sondern geteilt durch -a auf beiden seiten

---

Dann hättest du aber

0 = 72 ² + ( 32 / - a )

herausbekommen müssen ...