Brückenbogen 2 Meter über dem Boden (Parabeln). Bestimmen Sie die Entfernung zwischen diesen beiden Punkten.

Question

Die Lösungen liegen vor, doch ich hätte das gerne so erklärt, dass man es auch versteht.

Aufgabe:

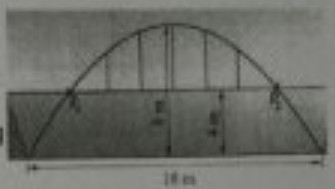
Ein Brückenbogen hat die Form eines Parabelbogens. Die Spannweite der Brücke beträgt 18 m, die Scheitelhöhe 8 m über dem Boden. Die Straße, die horizontal 4 m über dem Boden verlaufen soll, ist in den Punkten P_{1} und P_{2} des Brückenbogens befestigt. Bestimmen Sie die Entfernung zwischen diesen beiden Punkten.

Lösung:

Geeignetes Koordinatensystem festlegen; Z. B. x-Achse: Straßenquerschnitt, y- Achse durch Scheitelpunkt.

Mit \( \mathrm{S}(4 \mid 0) \) und \( P(9 \mid-4) \) ergibt sich die Parabelgleichung: \( f(x)=-\frac{8}{81} x^{2}+4 \).

\( \mathrm{P}_{4}(-\sqrt{40,5} \mid 0) \) und \( \mathrm{P}_{2}(\sqrt{40,5} \mid 0) \) und damit eine Entfemung von \( 2 \sqrt{40,5} \mathrm{~m}=12,7 \mathrm{~m} \).

Answer 1

Einen Bogen der Höhe h mit der Spannweite w kannst du wie folgt Modellieren

f(x) = h - h/(w/2)^2·x^2 = 8 - 8/(9)^2·x^2 = 8 - 8/81·x^2

Die Straße in der Höhe 4 kann modelliert werden über

g(x) = 4

Jetzt braucht man Schnittpunkte (nur x-Koordinate) und setzt f(x) = g(x)

8 - 8/81·x^2 = 4
x = ± 9/2·√2

Der Abstand dieser Stellen ist 2 * 9/2·√2 = 12.73 h

Scheu dich nicht dir eine Skizze zu machen und dir immer das zu verbildlichen, was du da gerade ausrechnest.