Nun,
für beide Verfahren stellst Du die (Un)Gleichungen auf
400 x + 900 y -> max
{3x + y ≤ 21, 3x + 3y ≤ 24, x + 3y ≤ 22}
dann zeichnest Du die Ungleichungen und verschiebst die Zielfunktion auf einen der Eckpunkte,
etwa so
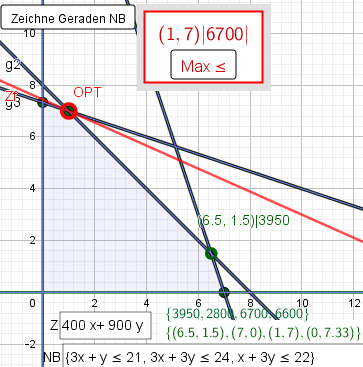
https://www.geogebra.org/m/weyhrbrq
für dem Simplex machst Du aus den Ungleichungen (Schlupfvariablen einführen) Gleichungen
{3x + y +s1 = 21, 3x + 3y + s2 = 24, x + 3y + s3 = 22}
und packst das in ein Tableau, etwa
\(\small \left(\begin{array}{rrrrrr}3&1&1&0&0&21\\3&3&0&1&0&24\\1&3&0&0&1&22\\-400&-900&0&0&0&0\\\end{array}\right)\)
das Verfahren ist im Link beschrieben und führt auf das Endtableau
\(\small \left(\begin{array}{rrrrrr}0&0&1&-\frac{4}{3}&1&11\\1&0&0&\frac{1}{2}&-\frac{1}{2}&1\\0&1&0&-\frac{1}{6}&\frac{1}{2}&7\\0&0&0&50&250&6700\\\end{array}\right)\)
https://www.geogebra.org/m/fP8cnZbb
Wenn Du Detailfragen hast lass hören...
