Hier der Graph der Durchflußrate
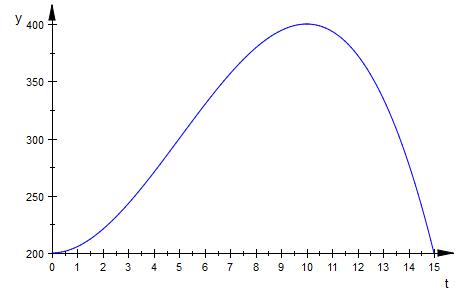
Die Durchflussrate d eines Flusses wird in den ersten 16 Minuten nach Beginn eines Unwetters erfasst durch
d(t) = - 2/5t^3 + 6t^2 + 200.
1) Wann ist die Durchflussrate maximal? Wie groß ist sie zu diesem Zeitpunkt?
Frage nach dem Extrempunkt
d ´( t ) = 0
t = 10 min
2) Wann ändert sich die Durchflussrate am stärksten?
Frage nach dem Wendepunkt
d ´´ ( t ) = 0
t = 5 min
3) Wann erreicht die Durchflussrate die Alarmgröße 250m3/min? Zu welcher Zeit beginnt der Alarm? Wie lange dauert der Alarm? Lösen Sie dies angenähert mit Hilfe von Testeinsetzungen.
d ( 10 ) = 400 m^3 / min
d ( 0 ) = 200 m^3 / min ( gefunden )
und jetzt muß man nach rechts durch Testeinsetzung den Alarmwert
finden
t = 15 min
Bei Bedarf nachfragen.