Erklären und lösen einer (kumulierten?) Binomialverteilung

Question

Aufgabe:

Die Schreibweise tut mir leid!:) ich hoffe ihr versteht es so. Im Prinzip ist es das Sigma Zeichen, wo oben 25 und unten k=10 steht, darauf folgt 25 über k und dann geht’s normal mit der Formel der binomialverteilung weiter.

$$\sum \limits_{k=10}^{25} \begin{pmatrix} 25\\k \end{pmatrix} \cdot 0.2^k \cdot (1 - 0.2)^{25-k}$$

Problem/Ansatz:

Ich soll die Formel in Worte fassen und die Wahrscheinlichkeit berechnen, aber ich verstehe nicht wie. Ich habe erst gedacht dass das eine kumulierte Binomialverteilung ist aber da darf doch unten im Sigma Zeichen nur eine 0 stehen? Kann mir da vielleicht einer weiterhelfen? Danke schonmal:)

Answer 1

Die Summe berechnet die Wahrscheinlichkeit, bei der 25-fachen Durchführung eines Bernoulli-Experiments mit der Trefferwahrscheinlichkeit 0,2 mindestens 10 Treffer zu erzielen.

Answer 2

Ich habe erst gedacht dass das eine kumulierte Binomialverteilung ist aber da darf doch unten im Sigma Zeichen nur eine 0 stehen?

Nein, hier gibt ja das k an, wie viele von den 25 Versuchen mit einem Treffer enden.

Wenn das k von 10 bis 25 geht, werden hier die Wahrscheinlichkeiten addiert von

10 Treffer
11 Treffer

....

25 Treffer, also werden alle Ergebnisse mit mindestens 10 Treffern berücksichtigt.

Answer 3

Ich habe erst gedacht dass das eine kumulierte Binomialverteilung ist aber da darf doch unten im Sigma Zeichen nur eine 0 stehen? Kann mir da vielleicht einer weiterhelfen? Danke schonmal:)

Ja das könnte man leicht denken, weil die kumulierte Binomialverteilung als Tabellenwerk oder auch in Taschenrechnern die Wahrscheinlichkeiten bestimmt das höchstens k Treffer eintreten

F(k) = P(X ≤ k)

Man kann aber tatsächlich auch über beliebige Intervalle summieren. Dabei gilt

P(a ≤ X ≤ b) = P(X ≤ b) - P(X ≤ a - 1) = F(b) - F(a - 1)

Bei dir Summiert man über das Intervall von 10 bis 25 Treffern. Das würde man also über eine Tabelle wie folgt berechnen:

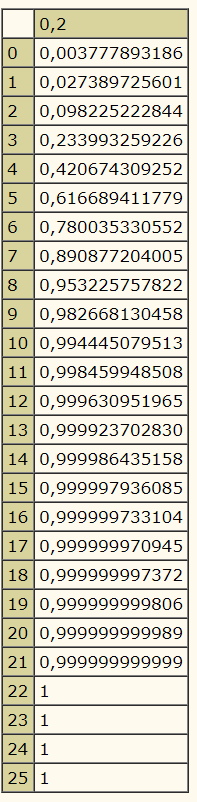
P(10 ≤ X ≤ 25) = P(X ≤ 25) - P(X ≤ 9) = F(25) - F(9) = 1 - 0,982668130458

Hier noch ein Tabellenauszug