Wie löse ich quadratische Gleichungen

Question

Aufgabe: \(x^2-7x=-6\)

Problem/Ansatz: ich weiß nicht wie ich diese Aufgabe lösen soll. Im Unterricht hatten wir so eine ähnliche Aufgabe in Klammern gesetzt und dann die Wurzel gezogen, habe keine Ahnung wie die Aufgabe zu lösen ist

Answer 1

Hallo,

ich nehme an, die Gleichung sieht so aus:

$$x^2-7x=-6$$

und das Thema ist Quadratische Ergänzung.

Du gehst dann so vor:

Aus der linken Seite der Gleichung soll eine Form wie (x - ?)² entstehen.

Du wendest die 2. Binomische Formel an. ? = die Hälfte der Zahl vor dem x, hier also -3,5

(x - 3,5)²  = -6 + ...

Wenn du die Klammer auflöst, erhältst du \(x^2-7x+12,25\).

12,25 war vorher nicht da und muss daher auch auf der anderen Seite der Gleichung addiert werden:

\((x-3,5)^2=-6+12,25\\ (x-3,5)^2=6,25\)

Jetzt wird auf beiden Seiten die Wurzel gezogen:

\(x-3,5=2,5\\ x= 6\\\text{oder}\\ x-3,5=-2,5\\ x=1\)

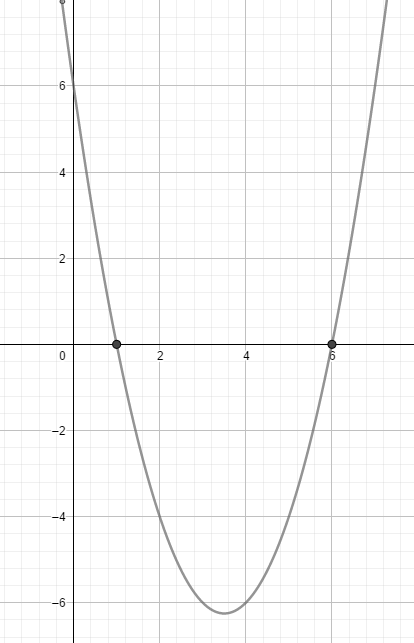
Damit hast du die Schnittpunkt der Parabel mit der x-Achse berechnet.

Gruß, Silvia

Answer 2

x^2-7x=-6

Aus der linken Seite die 2. binomische Formel machen:

x^2-2*x*3,5=-6

Quadratische Ergänzung:

x^2-2*x*3,5+3,5^2=-6+3,5^2

(x-3,5)^2=-6+12,25

(x-3,5)^2=6,25

(x+3,5)^2=2,5^2

x-3,5=2,5 oder x-3,5=-2,5

x=6   oder   x=1

Habt ihr es so gemacht oder mit pq-Formel?

Comments

Ich finde es jetzt bisschen unangenehm aber es ist so dass ich als Quereinsteiger in die 12 Klasse gekommen bin und die Klasse hat mit dem Thema in der 11 angefangen und führen es jetzt fort. Ich bin nicht wirklich mitgekommen fand es bisschen zu kompliziert die Lehrerin hat mich gar nicht so wirklich im Thema gebracht oder wie man das ganze berechnet etc. naja... und deswegen kann ich die Frage nicht wirklich beantworten

---

Es gibt verschiedene Möglichkeiten, quadratische Gleichungen zu lösen.

- Quadratische Ergänzung

- Lösungsformel ("pq-Formel")

- Satz des Vieta bei ganzzahligen Lösungen.

Übrigens ist das eigentlich schon Thema in der 8. Klasse...

:-)

Vergleiche die Antworten hier doch einmal mit deinen Aufzeichnungen.

Answer 3

x^2-7x+6=0

Satz von Vieta:

(x-6)(x-1) = 0

x1=6

x2= 1