Was bedeutet diese Funktion/Schaubild? f(x) = { x^2 ; x ≤ 1 neue Zeile (x - 2)^2 ; x > 1}

Question

Gegeben:

\( f(x) = \left\{\begin{array}{l}x^{2} ; \quad x \leq 1 \\ (x-2)^{2} ; \quad x>1\end{array}\right\} \)

Sind das nur Hinweise oder ist das eine oder mehrere Funktion(en)?

Was bedeutet diese Funktion/Schaubild?

Answer 1

Hallo Afrob,

 

wenn da also steht

f(x) =

{ x² ; x ≤ 1

(x - 2)² ; x > 1}

 

dann bezeichnet das eine Funktion.

Für alle x ≤ 1 musst Du die Funktionsvorschrift x² anwenden, um f(x) zu errechnen,

für alle x > 1 musst Du die Funktionsvorschrift (x - 2)² anwenden, um f(x) zu errechnen.

 

An der Stelle x = 1 ändert sich also für ein und dieselbe Funktion f(x) die Funktionsvorschrift:

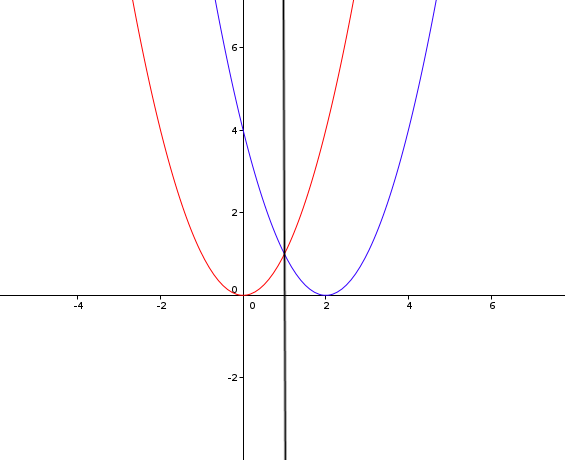
Links der schwarzen senkrechten Linie und bis zu dieser Linie einschließlich wird f(x) durch den roten Graphen dargestellt, rechts der schwarzen Linie wird f(x) durch den blauen Graphen dargestellt.

 

Alles klar?

 

Besten Gruß

Comments

Vielen Dank, habs jetzt verstanden - wie immer, wenn du mir etwas erklärst :)

Danke auch an Unknown. :)

Answer 2

Hi Afrob,

das ist eine zusammengesetze Funktion.

Für alle Stellen bis x = 1 gilt der obere Teil, ab dann gilt der untere Teil. Das sieht dann so aus:

 

Grüße