Hallo,
Ich weiß, dass man der Richtungsvektor der Geraden orthogonal zum Normalenvektor der Ebene stehen muss, ...
Ja - das ist schon mal das wichtigste. Die Parameterform einer Geraden ist gegeben durch einen Punkt \(P\) und einen Richtungsvektor \(r\). \(P\) mit \(P=(4|\,9|\,7)\) ist bereits gegeben, also fehlt noch \(r\). Und wie Du schon richtig fest gestellt hast, muss \(r\) senkrecht auf \(n\), dem Normalenvektor der Ebene \(E\), stehen. $$E: \quad 2x_1 + x_2 - 2x_3 = 12, \quad \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} x = 12$$Also ist $$ n = \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} $$ 'Senkrecht auf..' heißt in diesem Fall, dass das Skalarprodukt beider Vektoren gleich 0 sein muss. Also ist ein Vektor \(r\) gesucht, für den gilt$$n \cdot r = 0$$Dafür gibt es beliebig viele Lösungen. Man findet eine Lösung, indem man eine Koordinate von \(n\) auf \(0\) setzt, die beiden anderen vertauscht und eine der beiden negiert. Ich setze mal die dritte Koordinate zu \(0\)$$n= \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} \to \begin{pmatrix}2\\ 1\\ 0\end{pmatrix} \to r = \begin{pmatrix}-1\\ 2\\ 0\end{pmatrix}$$Probiere es aus. Wenn Du die Summe der Koordinatenprodukte bildest, kommt immer \(0\) heraus. Ich setze die zweite Koordinate mal auf \(0\)$$n= \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} \to \begin{pmatrix}2\\ 0\\ -2\end{pmatrix} \to r = \begin{pmatrix}2\\ 0\\ 2\end{pmatrix}$$Ich habe Dir beide Lösungen hier mal gezeichnet
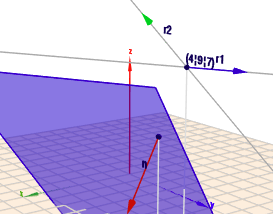
Klick auf das Bild, dann öffnet sich die Szene im Geoknecht3D, und Du kannst sie mit der Maus rotieren und bekommst so einen räumlichen Eindruck. Und nutze das Mausrad, um den Zoom zu ändern.
Es gibt natürlich noch beliebig viele andere Lösungen. Wähle zwei der drei Koordinaten von \(r\) beliebig und rechne die dritte aus. Z.B.: \(r_1=1\) und \(r_2=2\):$$n \cdot r = 2 \cdot (r_1=1) + 1 \cdot (r_2=2) - 2 r_3 = 0 \implies r_3 = 2 \\ \implies r = \begin{pmatrix}1\\ 2\\ 2\end{pmatrix}$$Frage bitte nach, wenn es nicht 'idiotensicher' war ;-)