Wie du evtl am Nachrechnen feststellst erleichtert die Zusammenfassung der Faktoren die Polynomdivision nicht erheblich.
Denke eventuell über die Benutzung des Horner Schemas nach, auch wenn du dieses dann zweifach machen musst.
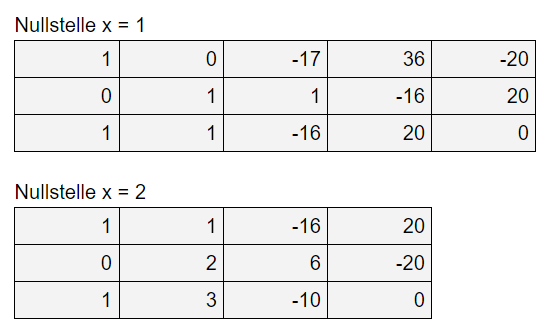
Ich persönlich finde das von Aufwand wesentlich einfacher. Aber das darf man nur machen, wenn die Methode freigestellt ist. Bzw. das Horner Schema erlaubt ist.
Die Nullstellen des restlichen Faktors x^2 + 3·x - 10 = 0 sollten dann leicht sein. pq-Formel, abc-Formel, Satz von Vieta oder quadratische Ergänzung sind leicht möglich.