Quadratische Ergänzungen lösen

Question

Aufgabe:

Löse die Gleichungen durch quadratisches Ergänzen. Bringe die Gleichungen, wenn nötig, zunächst auf die Form x² + px + q = 0

a) x²-6x = 9

b) x² = 40-16x

c) x² -20 = 8x

d) x² + 7x = 26

e) 4 - x² = 10

f) 2x² -12 = 3x

Problem/Ansatz:

Leider verstehe ich diese Aufgabe nicht, und weiss nicht wie man quadratisches Ergänzen genau anwendet. Könnte mir das vielleicht einer erklären und die Aufgaben lösen? !

Answer 1

Das quadratische Ergänzen ist im Prinzip das "Ergänzen" eines gegebenen Polynoms zu einem Resultat einer binomischen Formel, welches dann mithilfe dieser umgeformt werden kann. Diese ist im Übrigen auch wichtig zur Herleitung der bekannten pq-Formel / abc-Formel.

$$\text{Beispiel: } x^2-16x = (x^2-16x+64)-64 = (x-8)^2-64$$

Hier als Beispiel mal a)-c), die anderen Aufgaben kannst du dann sicher auch. (Bei e) eventuell ein x vergessen?)

a)

$$x^2-6x=9 \Rightarrow x^2-6x+9=18 \Rightarrow (x-3)^2=18 \Rightarrow |x-3|=\sqrt{18}=3\sqrt{2} \\ \Rightarrow x_1-3=3\sqrt{2} \ \wedge \ x_2-3=-3\sqrt{2} \Rightarrow x_1=3+3\sqrt{2} \ \wedge \ x_2=3-3\sqrt{2}$$

b)

$$x^2=40-16x \Rightarrow x^2+16x-40=0 \Rightarrow x^2+16x+64-64-40=0 \\ \Rightarrow (x+8)^2-104=0 \Rightarrow (x+8)^2=104 \Rightarrow |x+8|=\sqrt{104}=2\sqrt{26} \\ \Rightarrow x_1+8=2\sqrt{26} \ \wedge \ x_2+8=-2\sqrt{26} \Rightarrow x_1=2\sqrt{26}-8 \ \wedge x_2=-2\sqrt{26}-8$$

c)
$$x^2-20=8x \Rightarrow x^2-8x-20=0 \Rightarrow x^2-8x+16-16-20=0 \\ \Rightarrow (x-4)^2-36=0 \Rightarrow (x-4)^2=36 \Rightarrow |x-4|=\sqrt{36}=6 \\\Rightarrow x_1-4=6 \ \wedge \ x_2-4=-6 \Rightarrow x_1=10 \ \wedge x_2=-2$$

Comments

Kannst du noch d-f lösen? Danke (brauche es für morgen)

---

Ich würde dir vorschlagen es selbst zu probieren (dauert auch nicht lange), du hast neben mir in diesem Thread auch noch eine weitere Person, die deine Fragen beantworten kann.

Die Lösungen zum Vergleich sind

d) $$x_1=\frac{-7+3\sqrt{17}}{2} \ \wedge \ x_2=\frac{-7-3\sqrt{17}}{2}$$

e) Ich nehme an es heißt 4 - x² = 10x. $$x_1=\sqrt{29}-5 \ \wedge \ x_2=-\sqrt{29}-5$$

f) $$x_1=\frac{3+\sqrt{105}}{4} \ \wedge \ x_2=\frac{3-\sqrt{105}}{4}$$

Answer 2

Hallo,

ich rechne eine Aufgabe vor, die anderen versuche dann bitte selber zu lösen. Melde dich, falls du noch Fragen hast.

\(x^2-6x=9\)

Ziel ist es, eine Gleichung der Form

\((x\pm a)^2=b\) aufzustellen.

a ist die Hälfte der Zahl, die vor dem x steht (p), hier also 3

Daraus ergibt sich

\((x-3)^2... = 9\)

Würden wir die Klammer ausrechnen, erhielten wir \(x^2-6x+9\). Um das "Gleichgewicht" zu halten, müssen wir 9 auch auf der rechten Seite der Gleichung addieren und erhalten \((x-3)^2=18\).

Jetzt auf beiden Seiten die Wurzel ziehen:

\(x-3=\pm\sqrt{18}\\ x=\pm\sqrt{18}+3\)

Jetzt nur noch die beiden Nullstellen ausrechnen:

\(x_1=\sqrt{18}+3=7,24\\x_2=-\sqrt{18}+3=-1,24\)

Graphisch stellt sich das so dar

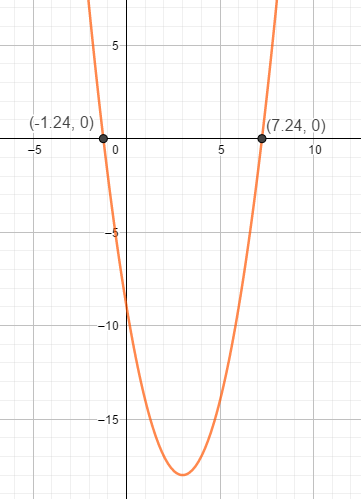
So kannst du auch die anderen Aufgaben lösen.

Gruß, Silvia

Answer 3

Die Augabenstellung macht für mich keinen Sinn. Entweder löse ich die Aufgabe über quadratische Ergänzung oder ich bringe sie auf die p,q Form.

a) x²-6x = 9

x²-6x +9= 9 +9
\( (x-3)^{2} \) =18

x₁=3+\( \sqrt{18} \) = 3+3*\( \sqrt{2} \)

x₁=3 - \( \sqrt{18} \) = 3 - 3*\( \sqrt{2} \)

b) x² = 40-16x

x²+16x+64 =104

\( (x+8)^{2} \) = 4*26

x₁= -8 +2*\( \sqrt{26} \)

x₂= -8 -2*\( \sqrt{26} \)

c) x² -20 = 8x

x²-8x+16=20+16
\( (x-4)^{2} \) =36

x₁= 4+6=10

x₂ = 4-6 = -2

d) x² + 7x = 26

x²+ 7x + 49/4 =153/4=9/4 * 17
x₁= - 7/2 +3/2 * \( \sqrt{17} \)

x₂  = = - 7/2 - 3/2 * \( \sqrt{17} \)

e) 4 - x² = 10

x²= - 6 nicht im R zu lösen

f) 2x² -12 = 3x

x²- 3/2 x +9/16 = 6 9/16

x₁= 3/4 +1/4 \( \sqrt{105} \)

x₂= 3/4 - 1/4 \( \sqrt{105} \)

Comments

Tja genau so ist die Aufgabenstellung im Buch :D

Answer 4

Bringe zunächst die Gleichung in die Form

x^2 + px = - q

Das schaffst du oder? Addiere dann auf beiden Seiten die quadratische Ergänzung die aus der linken Seite einen ausmultiplizierten binomischen Term macht.

x^2 + px + (p/2)^2 = (p/2)^2 - q

Die linke Seite fasst man zu einem Quadrat eines Binoms zusammen, die rechte Seite fasst du gleich zusammen.

(x + p/2)^2 = (p/2)^2 - q

Jetzt ziehst du auf beiden Seiten die Wurzel

x + p/2 = ± √((p/2)^2 - q)

Und subtrahierst noch auf beiden Seiten das p/2

x = - p/2 ± √((p/2)^2 - q)

Hier sind die Beispiele

a)
x^2 - 6·x = 9
x^2 - 6·x + 9 = 18
(x - 3)^2 = 18
x - 3 = ± √18
x = 3 ± √18 → x = -1.243 ∨ x = 7.243

b)
x^2 = 40 - 16·x
x^2 + 16·x = 40
x^2 + 16·x + 64 = 104
(x + 8)^2 = 104
x + 8 = ± √104
x = - 8 ± √104 → x = -18.20 ∨ x = 2.198

c)
x^2 - 20 = 8·x
x^2 - 8·x = 20
x^2 - 8·x + 16 = 36
(x - 4)^2 = 36
x - 4 = ± 6
x = 4 ± 6 → x = - 2 ∨ x = 10

d)
x^2 + 7·x = 26
x^2 + 7·x + 12.25 = 38.25
(x + 3.5)^2 = 38.25
x + 3.5 = ± √38.25
x = - 3.5 ± √38.25 → x = -9.685 ∨ x = 2.685

e)
4 - x^2 = 10 → Hier fehlt der lineare Term mit x und dafür hat man 2 konstante Terme. Ist das richtig?

f)
2·x^2 - 12 = 3·x
x^2 - 6 = 1.5·x
x^2 - 1.5·x = 6
x^2 - 1.5·x + 0.5625 = 6.5625
(x - 0.75)^2 = 6.5625
x - 0.75 = ± √6.5625
x = 0.75 ± √6.5625 → x = -1.812 ∨ x = 3.312