Geometrische Darstellung von Vektoren in R^3

Question

Aufgabe:

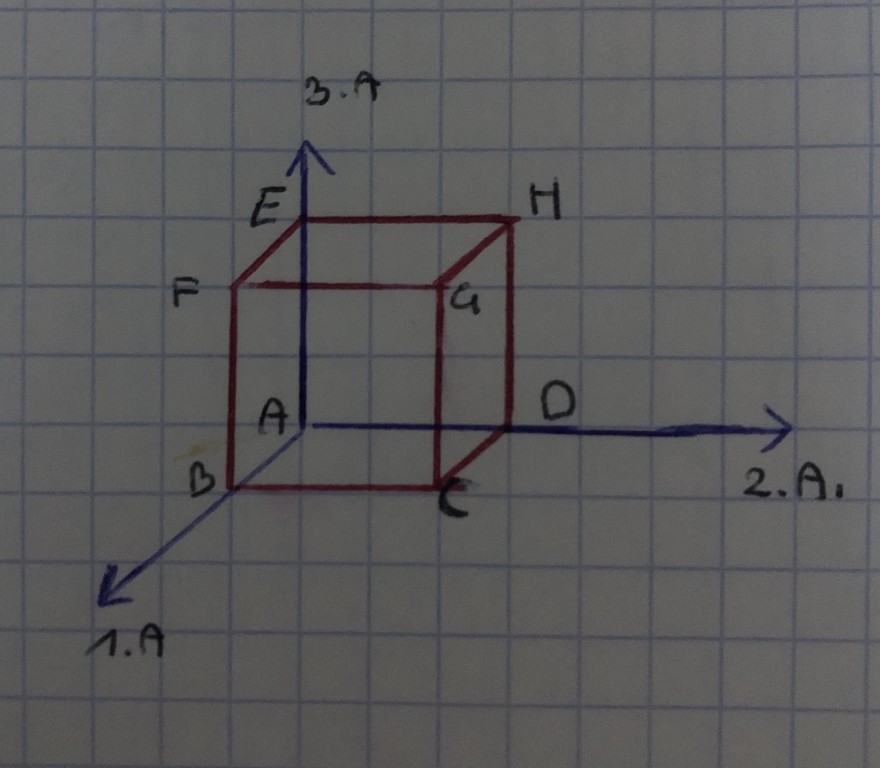
Die untenstehende Abbildung zeigt einen Würfel mit der Kantenlänge 6, dessen Eckpunkt A im Ursprung des Koordinatensystems liegt.

a) Gib die Koordinaten aller Würfeleckpunke an!

b) Verschiebe den Würfel so, dass der Würfelmittelpunkt M im Punkt M₁ = (4 | 1 | 6) zu liegen kommt! Welche Koordinaten haben die einzelnen Eckpunkte dann?

Beispiel a) habe ich schon gelöst: A = (0/0/0), B = (6/0/0), C = (6/6/0), D = (0/6/0), E = (0/0/6), F = (6/0/6), G = (6/6/6), H = (0/6/6)

Bei Beispiel b komme ich leider nicht weiter..

Vielen Dank im Voraus für eure Hilfe!

Answer 1

Hallo Peter,

bestimme den Vektor \(\vec v\), um den der Würfel verschoben wird, indem Du vom neuen Mittelpunkt \(M_1 (4|1|6)\) den alten Mittelpunkt \(M (3|3|3)\) abziehst:$$\vec v = \vec{MM_1} = M_1 - M = \begin{pmatrix}4\\ 1\\ 6\end{pmatrix} - \begin{pmatrix}3\\ 3\\ 3\end{pmatrix} = \begin{pmatrix}1\\ -2\\ 3\end{pmatrix}$$nun addiere \(\vec v \) zu jedem der anderen Punkte hinzu. So erhältst Du die Eckpunkte des verschobenen Würfels

zum Beispiel: $$B_1 = B + \vec v = \begin{pmatrix}6\\ 0\\ 0\end{pmatrix} + \begin{pmatrix}1\\ -2\\ 3\end{pmatrix} = \begin{pmatrix}7\\ -2\\ 3\end{pmatrix}$$ (klick auf das Bild und zoome mit dem Mausrad)

Answer 2

Der Mittelpunkt des ersten Würfels liegt bei M1(3|3|3).

Von M1 nach M2(4|1|6) wir der Würfel um v=[1|-2|3] verschoben.

Du musst nun jeden Eckpunkt um v verschieben.

:-)