Für welche Winkelgröße \alpha wird das entstehende Dreieck gleichschenklig?

Question

Aufgabe:

Das Dreieck ABC hat die in der Figur abgebildeten Eigenschaften.
Für welche Winkelgröße \( \alpha \) wird das entstehende Dreieck gleichschenklig?

Meine Idee:

Also da ja das Dreieck AMC gleichschenklig ist, muss ja dann gelten, dass alpha = 2 beta gilt. Aber damit das gesamt Dreieck gleichschenklich wird, muss ja alpha = beta betragen. Also ist die Aufgabe nicht lösbar?

Answer 1

Hallo,

Also da ja das Dreieck AMC gleichschenklig ist, muss ja dann gelten, dass alpha = 2 beta gilt.

wenn Du \(\beta = 2 \alpha\) meinst, dann ist das richtig!

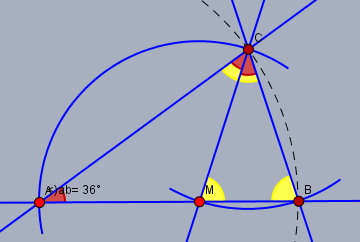
Aber damit das gesamt Dreieck gleichschenklich wird, muss ja alpha = beta betragen

Nur wenn die Basis \(AB\) sein soll, das steht aber nirgends. Nimmt man dagegen \(BC\) als Basis des gleichschenkligen Dreiecks, dann muss \(\gamma = \beta\) sein.

Jetzt noch fix die Winkelsumme im Dreieck gebildet$$\alpha + \beta + \gamma = \alpha + 2\alpha + 2\alpha = 5 \alpha = 180° $$... und \(\alpha = 36°\)

PS.: das Verhältnis Länge des Schenkels zur Länge der Basis ist hier der goldene Schnitt $$\frac{|AB|}{|BC|} = \Phi = \frac 12(1+\sqrt 5)$$

Comments

Muss es nicht beta =2*alpha heißen?

---

Muss es nicht beta =2*alpha heißen?

Ja sicher doch. Voll drüber gelesen würde ich sagen .. ;-)

Answer 2

Also ist die Aufgabe nicht lösbar?

Was wäre mit alpha = 36 Grad

Kannst du damit mal alle Winkel durchrechnen?

Im zweiten schritt könntest du alle Winkel mal in Abhängigkeit von alpha beschriften. Dann müsstest du auch eine Bedingung aufstellen können denke ich.