Kann man diese Aufgabe auch via Pythagoras lösen?
Kann man, ist aber aufwendiger und führt auf den identischen Lösungsweg ...
Für den Pythagoras braucht man ja ein rechtwinkliges Dreieck ...
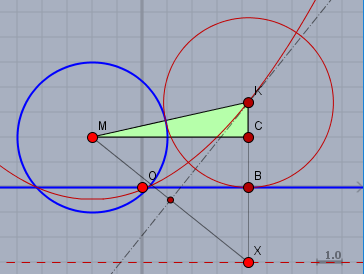
... hier \(\triangle MCK\). Der blaue Kreis ist gegeben \(M=(m_x|\, m_y), \space r\) und soll vom gesuchten Kreis \(k\) (rot) berührt werden. Der Mittelpunkt von \(k\) sei \(K=(x|\,y)\) und sein Radius ist \(|y|\). Es gilt$$|KC| = y - m_y \\ |MC| = x - m_x \\ |MK| = y + r $$Die dritte Bedingung folgt aus der Forderung, dass \(k\) den blauen Kreis berühren soll, und da \(y\) der Radius von \(k\) ist, ist die Entfernung der Mittelpunkte eben die Summe der Radien.
Jetzt den Pythagoras angewendet und umgeformt:$$\begin{aligned}|MK|^2 &= |MC|^2 + |KC|^2 \\ (y + r)^2 &= (x - m_x)^2 + (y - m_y)^2 \\ y^2 + 2yr + r^2 &= (x - m_x)^2 + y^2 - 2ym_y + m_y^2 \\ 2yr + 2ym_y &= (x - m_x)^2 + m_y^2 - r^2\\ 2y(m_y + r) &= (x - m_x)^2 + (m_y^2 - r^2) &&\left|\, \div 2(m_y + r) \right.\\ y &= \frac 1{m_y + r} (x - m_x)^2 + \frac 12(m_y - r) \end{aligned}$$Und diese Gleichung sollte Dir bekannt vorkommen, wenn Du mal einen Blick auf meine Antwort oben wirfst. Es geht dann weiter wie oben beschrieben.
Vorher kann man sich noch Gedanken machen, wo denn die andere Parabel geblieben ist. Es steht ja nirgends, dass sich \(k\) oberhalb der X-Achse befinden muss. Dazu folgende Zeichnung:
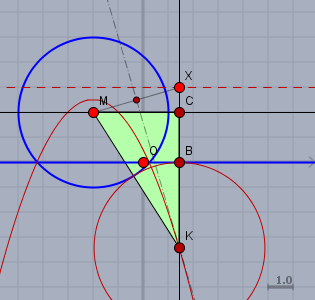
Hier ist $$|KC| = m_y -y\\ |MC| = x - m_x \\ |MK| = -y + r$$die weitere Rechnung ist wie oben, nur mit teilweise geänderten Vorzeichen.
PS.: habt Ihr noch keine Parabeln durchgenommen? ;-)