Bestimmen Sie die Parameter a und b in der Funktionsgleichung von g.

Question

Aufgabe: Design einer Flasche

Problem/Ansatz:

Hab bei der a) und b) hab ich raus:

g(x)= 1/25x^2+2

f(x)=3

h(x)=75/x^2

Bei der c) hab ich dann 356,43 VE raus

Und bei der d) 91,6 FE

Ist das richtig ????

Aufgabe:

Design einer Flasche

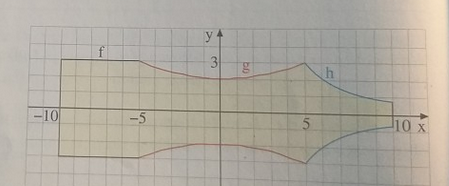
Ein neues Flaschenmodell wird durch einen \( 5 \mathrm{cm} \) langen Zylinder f mit einem Durchmesser von \( 6 \mathrm{cm}, \) einem \( 10 \mathrm{cm} \) langen eingebuchteten Mittelteil g und einem \( 5 \mathrm{cm} \) langen Flaschenhals h gebildet.

Die Ausgussöffnung am Flaschenhals hat einen Durchmesser von \( 1,5 \mathrm{cm} . \)

Die beiden Funktionen \( g(x)=a x^{2}+b \) und \( h(x)=\frac{c}{x^{2}} \) modellieren dabei die gebogenen Randkurven \( \mathrm{f} \) und \( \mathrm{g} \).
a) Bestimmen Sie die Parameter a und b in der Funktionsgleichung von g.
b) Bestimmen Sie den Parameter c in der Funktionsgleichung von h.
c) Berechnen Sie nun das Volumen der Flasche.
d) Wie groß ist die abgebildete, gelb markierte Querschnittsfläche A der Flasche?

Answer 1

Alles fast richtig nur zweimal nicht gerundet sondern nur abgeschnitten.

Also

356.44 und 91.67 wenn du richtig runden würdest.

Comments

Wie berechnet man bei der c) das Volumen? Also ich verstehe nicht, welche Funktion man dafür nehmen muss.

---

Für c) kannst du zum einen einen Zylindernehmen für den unteren Teil.

Ein Rotationsintegral mit der Funktion g(x) = 1/25x^2+2 für den mittleren Teil.

Und ein Rotationsintegral mit der Funktion h(x) = 75/x^2 für den oberen Teil.

Willst du das mal probieren?

---

Was ist mit dem Zylinder im unteren Teil gemeint? Die anderen beiden Rotationsintegralen verstehe ich!

---

s. Skizze, blauer Zylinder

---

Schöne Skizze. Ich hoffe die Fragestellerin kann den Zylinder dort erkennen. Das Volumen eines Zylinders ist

V = pi * r^2 * h

Man könnte den Zylinder aber auch mit einem Rotationsintegral mit der Funktion f(x) = 3 berechnen. Zumindest wenn du das besser verstehst als einen einfachen Zylinder.

---

Danke, das hat mir sehr geholfen!!

Bezüglich der d) noch eine letzte Frage:

Mit welcher Formel muss ich hier rechnen? Ich habe erst gedacht, ich integriere die Funktionen nur ohne pi, da es hier ja dann nicht um das Volumen geht, da bin ich aber nicht auf das Ergebnis gekommen.

---

Hast du vorher auch \((g(x))^2\) und \((h(x))^2\) berechnet?

---

Vielleicht nur vergessen mit 2 zu multiplizieren.

d)

2·(∫ (-10 bis -5) (3) dx + ∫ (-5 bis 5) (1/25·x^2 + 2) dx + ∫ (5 bis 10) (75/x^2) dx = 275/3 = 91.67 cm²