Zeigen Sie durch das Lösen eines Optimierungsproblems

Question

ich habe eine Aufgabe wie unten,

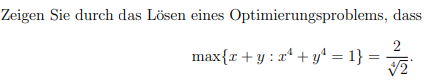
Text erkannt:

Zeigen Sie durch das Lösen eines Optimierungsproblems, dass
$$ \max \left\{x+y: x^{4}+y^{4}=1\right\}=\frac{2}{\sqrt[4]{2}} $$

und hier ist meine Lösung. Ist f(x,y) = x+y unter Bedingung g(x,y) = x⁴+y⁴-1 oder umgekehr?

Ich bin nicht sicher, ob meine Lösung richtig ist..

Text erkannt:

Kritische Punfie im Innern E sind die Purkt ( \( x, 0 \) ) mith
Wir foser \( \quad f=(x+y) \)
Neberbedingung \( : x^{4}+y^{4}=1 \)

Answer 1

Lagrange Funktion
L(x, y, k) = x + y - k·(x^4 + y^4 - 1)

Partielle Ableitungen
L'x(x, y, k) = 1 - 4·k·x^3 = 0 → k = 0.25/x^3
L'y(x, y, k) = 1 - 4·k·y^3 = 0 → k = 0.25/y^3

Gleichsetzen
0.25/x^3 = 0.25/y^3 → y = x

In Nebenbedingung einsetzen
x^4 + x^4 = 1 → x = y = 2^(3/4)/2

Maximum
x + y = 2^(3/4)/2 + 2^(3/4)/2 = 2^(3/4)

Comments

Achja, vielen Dank, deine Lösung ist viel mehr besser.