Von einem rechteckigen

Question

Aufgabe:

Hallo,

ich habe ein Problem bei folgender Aufgabe:
Von einem rechteckigen Plakat mit den Seitenlängen 100 cm(Seite a) und 60 cm(Seite b) wurde eine Ecke abgeschnitten(10 cm(aus Seite a)⋅4 cm(aus Seite b)). Aus dem Rest soll nun ein rechteckiges Stück mit möglichst großem Flächeninhalt zugeschnitten werden. Welche Maße hat dieses rechteckige Stück.

Extremal werden soll ja der Flächeninhalt, also A(x;y)=(100-x)(60-y), wobei x und y die Differenz der jeweiligen Seitenlängen des neuen Rechteckes im Vergleich zum alten Rechteck sind.

Nur leider komme ich einfach überhaupt nicht auf die Nebenbedingung. Kann mir jemand da vielleicht einen entscheidenden Tipp geben?

Problem/Ansatz: Ich weiß, dass -0,4x^2+96x als Zeilfunktion raus kommt aber warum verstehe es einfach nicht bitte helfen

Answer 1

Die Fläche des zu optimierenden Rechtecks ist A(x)=(60-x)(90+2,5x).

Die Nullstelle der ersten Ableitung in die Flächenformel einsetzen, ergibt die größte Rechtecksfläche.

Answer 2

Ich würde die Ecke nach oben rechts legen.

Dann ist g(x)= 60 - 0,4( x-90) = 96 - 0,4 x

mit 90 ≤ x ≤ 100

Rahmenbedingung A=56*100=5600 cm²

                               B= 60*90= 5400 cm²

F(x) = x * g(x)= - 0,4 x²+96 x

F'( x) = - 0, 8 x + 96 = 0

x = 120 , doch das ist außerhalb des Intervalls

A(max) = 5600 cm²

Comments

Wie kommst du auf 0,4x^2

---

4cm auf 10cm = 4/10 =0,4

Das sind die Maße für das rausgebroche Dreieck.

Von einem rechteckigen Plakat mit den Seitenlängen 100 cm(Seite a) und 60 cm(Seite b) wurde eine Ecke abgeschnitten(10 cm(aus Seite a)⋅4 cm(aus Seite b)).

---

Das Einfachste, wäre eine Zeichnung.  Das Zweiteinfachste ist, ich gebe die Koordinaten der Eckpunkte des zu betrachtenden Fünfecks an.

A(0;0)  B(100;0)  C( 100;56)

D(90 ; 60)  E ( 0; 60)

C und D liegen auf g

Answer 3

Hier mal ein Bild wie ein Bild wie ich es mir vorstelle

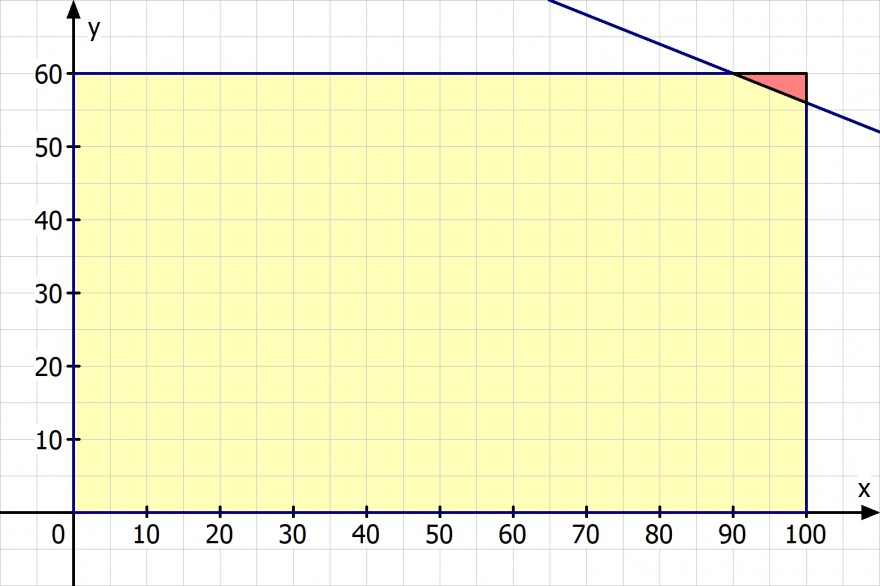
Du musst als erstes die Gerade modellieren, durch dei die abgetrennte Ecke markiert wird. Ich kenne zwei Punkte dieser Geraden

(90 | 60) und (100 | 56)

m = (56 - 60) / (100 - 90) = -0.4

y = -0.4·(x - 90) + 60
y = 96 - 0.4·x

Die Fläche des Rechtecks berechnet sich aus

A = x·y = x·(96 - 0.4·x) = 96·x - 0.4·x^2

Diese Zielfunktion müssen wir ableiten und null setzen

A' = 96 - 0.8·x = 0 --> x = 120

Das Maximum wäre also bei x = 120. Dieses liegt aber außerhalb des Definitionsbereiches. Unsere Funktion ist ja nur im Intervall [90 ; 100] gültig.

Also ist das Maximum unserer Funktion bei x = 100. Dieses ist ein sogenanntes Randmaximum.