Charakteristisches Polynom Drehmatrix ausrechnen

Question

Aufgabe:

Charakteristisches Polynom Dreh/Spiegelmatrix

Problem/Ansatz:

Ich weiß, dass das zb die Drehmatrix aussieht wie folgt:

Text erkannt:

\( Q=\left(\begin{array}{ll}\cos (\alpha) & -\sin (\alpha) \\ \sin (\alpha) & \cos (\alpha)\end{array}\right) \

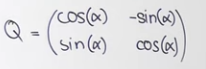
Ich weiß auch, dass die EW e^(+- i*alpha) sind.

Das charakteristische Polynom ist: (cos(alpha)-t)*(sin(alpha)-t) + sin(alpha)^2

Aber wie vereinfache ich dieses nun um an die EW (Nullstellen ) zu kommen? Leider bin ich nicht so gut im cos-sin rechnen...

Wäre lieb wenn mir jdm kurz den Rechenweg erklären könnte :)

Text erkannt:

\( Q=\left(\begin{array}{ll}\cos (\alpha) & -\sin (\alpha) \\ \sin (\alpha) & \cos (\alpha)\end{array}\right) \

Comments

Alternativ gilt allgemein für 2×2-Matrizen Q: det(Q - t·E₂) = t² - spur(Q)·t + det(Q).

Answer 1

Verwende den trigonometrischen Pythagoras \(\sin^2(\alpha)+\cos^2(\alpha)=1\)

Es gilt:$$(\cos(\alpha)-t)(\cos(\alpha)-t)+\sin^2(\alpha)=t^2-2t\cos(\alpha)+\underbrace{\sin^2(\alpha)+\cos^2(\alpha)}_{=1}\overset{!}=0$$D. h. du hast: \(t^2-2\cos(\alpha)t+1=0\). Darauf kannst die die pq-Formel anwenden. Dann gilt:$$t_{1,2}=\cos(\alpha)\pm \sqrt{\cos^2({\alpha})-1}=\cos(\alpha)\pm \sqrt{-\sin^2(\alpha)}=\cos(\alpha)\pm i \sin(\alpha)$$ Nun nur noch die eulersche Formel anwenden und fertig.

Comments

Vielen Dank! Jetzt wo ich die Lösung sehe, war es wirklich echt einfach :)

Answer 2

Aloha :)

Das charakteristische Polynom sieht in echt etwas anders aus:

$$\left|\begin{array}{c}\cos\alpha-t & -\sin\alpha\\\sin\alpha & \cos\alpha -t\end{array}\right|=(\cos\alpha-t)^2+\sin^2\alpha=\cos^2\alpha-2t\cos\alpha+t^2+\sin^2\alpha$$$$=(\cos^2\alpha+\sin^2\alpha)-2t\cos\alpha+t^2=t^2-2t\cos\alpha+1$$Die pq-Formel liefert die Eigenwerte:$$t_{1,2}=\cos\alpha\pm{\sqrt{\cos^2\alpha-1}}=\cos\alpha\pm\sqrt{{-\sin^2\alpha}}=\cos\alpha\pm i\sin\alpha$$

Comments

Danke :) Ja, bei de char. Polynom aufstellen war ich etwas abwesend :D